por raimundoocjr » Ter Jan 25, 2011 20:36
A priori não tenho uma base para início. Por favor ajudem-me, desde já obrigado.
-
raimundoocjr
-
por Renato_RJ » Ter Jan 25, 2011 21:22
Boa noite campeão...
Como sou fraco com geometria euclidiana vou perguntar, você tem a resposta ? Pois eu achei 90º, agora, como disse, sou fraco em geo, logo posso ter me enganado...
O chato é que terei que desenhar no PC para mostrar como cheguei aos 90º....
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-
Renato_RJ
- Colaborador Voluntário
-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
por LuizAquino » Qua Jan 26, 2011 09:53
Olá Pessoal,
Segue abaixo a construção auxiliar para resolver essa questão.
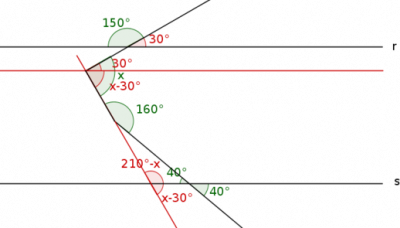
- Construção auxiliar
Para obter essa construção auxiliar você precisa dos conhecimentos sobre ângulos em retas paralelas cortadas por transversais. Veja as aulas do
Nerckie no YouTube sobre esse assunto:
Matemática - Aula 33 - Geometria Plana - Definições Preliminares - Parte 1http://www.youtube.com/watch?v=0DrV_i20J-cO endereço acima é da primeira parte. Ao todo são 4. Certifique-se de ver todas as partes.
Em seguida, usando o fato que em um triângulo o ângulo externo mede o mesmo que a soma dos dois ângulos internos não adjacentes a ele, teremos a equação:
(210°- x) + 40° = 160°
De onde obtemos, x=90°.
Agora, uma dica. Para desenhar figuras geométricas ou traçar gráficos de função (e muito mais coisa), conheçam o programa
GeoGebra. Foi com o GeoGebra que eu fiz a figura acima. Para um curso sobre esse programa, visite o meu canal no YouTube:
http://www.youtube.com/LCMAquino
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
por raimundoocjr » Qua Jan 26, 2011 15:07
Muitíssimo obrigado. O programa e o vídeo são muito bons.
-
raimundoocjr
-
por Renato_RJ » Qua Jan 26, 2011 21:54
Luiz, muito bom o vídeo...
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-
Renato_RJ
- Colaborador Voluntário
-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana] Qual é o comprimento "D" desse hexágono
por Marcosd » Qui Jan 28, 2016 15:24
- 4 Respostas
- 5896 Exibições
- Última mensagem por adauto martins
Dom Jan 31, 2016 20:26
Geometria Plana
-
- Geometria Plana - "Folhas sobrepostas"
por raimundoocjr » Qua Jan 26, 2011 21:21
- 2 Respostas
- 2059 Exibições
- Última mensagem por raimundoocjr
Qui Jan 27, 2011 15:40
Geometria Plana
-
- Geometria Plana - "Círculo Inscrito"
por raimundoocjr » Sáb Fev 12, 2011 16:18
- 2 Respostas
- 2078 Exibições
- Última mensagem por raimundoocjr
Dom Fev 13, 2011 09:15
Geometria Plana
-
- Geometria Plana - "Área Máxima"
por raimundoocjr » Sex Out 21, 2011 20:30
- 2 Respostas
- 4962 Exibições
- Última mensagem por saberdigitalnet
Sáb Nov 24, 2012 17:19
Geometria Plana
-
- Geometria Plana - "Valor de RQ"
por raimundoocjr » Ter Fev 15, 2011 21:54
- 2 Respostas
- 1954 Exibições
- Última mensagem por raimundoocjr
Qua Fev 16, 2011 13:49
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
