Tenho o seguinte problema:
Preciso encontrar o ângulo
 ou o ângulo
ou o ângulo  , para aplicar a função ArcTangente e obter o ponto A(x,y) pelos senos e cossenos...
, para aplicar a função ArcTangente e obter o ponto A(x,y) pelos senos e cossenos...Dados os pontos C e B, e o cateto b desejo obter o ponto A de modo que obtenha um triângulo retângulo.
o Ponto D obtenho facilmente pelos seno e cosseno dos ângulos obtidos pela função ArcTangente dos pontos C e B.
A distância do cateto "b" sempre será igual (valor fixo), mas a hipotenusa "a" é variável, bem como os pontos B e C tornando meu angulo
 sempre variável.
sempre variável.desde já agradeço...




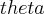 ou
ou 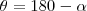 . E sim, não sei muito de programação mas testar se a reta CA é tangente deve ser um meio, só que talvez isso mude o problema pra quantidade de memória.
. E sim, não sei muito de programação mas testar se a reta CA é tangente deve ser um meio, só que talvez isso mude o problema pra quantidade de memória.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.