 por Rosana Vieira » Sáb Mar 03, 2012 18:44
por Rosana Vieira » Sáb Mar 03, 2012 18:44
Olá eu estou com dúvida para o item a
2.Um plano secciona um cubo de aresta medindo 9 cm, na terça parte das arestas que convergem para um mesmo vértice, dele retirando uma pirâmide triangular regular. Considere o poliedro que restou do cubo, depois de retiradas as 8 pirâmides pelas secções correspondentes aos 8 vértices do cubo.
a) Esboce uma planificação para este novo poliedro.
b) Calcule a distância entre duas faces triangulares opostas.
c) Calcule seu volume e a área de sua superfície.
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por timoteo » Dom Mar 04, 2012 04:13
por timoteo » Dom Mar 04, 2012 04:13
nao coloquei exatamente na terceira parte das arestas mas vc aproxima ai.
- Anexos
-
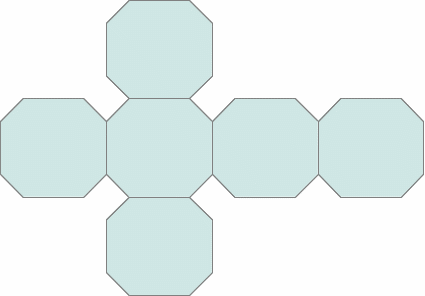
- planificaçao
- planificaçao_html_m2955969d.gif (6.83 KiB) Exibido 5524 vezes
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por Rosana Vieira » Seg Mar 05, 2012 00:22
por Rosana Vieira » Seg Mar 05, 2012 00:22
Olá Timoteo será que vc pode me ajudar com as formulas para o item b e c.
Obrigado pela dica do item a
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por timoteo » Seg Mar 05, 2012 08:35
por timoteo » Seg Mar 05, 2012 08:35
Rosana, para calcular os itens b e c o que é preciso de cara é encontrar a unidade de medida e que a questao ja informou,
u.
com isso e sabendo que as faces de cada piramide é dada por um triangulo retangulo de lados 1u e hipotenusa de
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
. é so utilizar as formuals de piramides. isso para questao c.
para a questao b, nao sei se estou entendendo bem mas pelo que entendi a distancia entre as faces opostas é de 2u.
boa sorte nos calculos.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por Rosana Vieira » Seg Mar 05, 2012 09:53
por Rosana Vieira » Seg Mar 05, 2012 09:53
Timoteo ainda eu não entedi o item b e c
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por timoteo » Seg Mar 05, 2012 20:58
por timoteo » Seg Mar 05, 2012 20:58
rosana eu fiz uma das oito piramides e dei a numeraçao acho que isso ira ajuda-la.
lembre-se que ao encontra a area e o volume de uma piramide vc deve multiplica-la por 8. e o mais importante, o que vc quer sao os valores do cubo sem as piramides, dai é so descontar.
- Anexos
-

- piramide
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por Aparecida » Seg Mar 05, 2012 22:19
por Aparecida » Seg Mar 05, 2012 22:19
Eu tambem quero ajuda nesse exercicio, nao tenho onde recorrer.
Li varias vezes enao entendo. se puder me explicar vou agradecer muito.
-
Aparecida
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Dom Out 30, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11735 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2846 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6143 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
-
- Geometria espacial
por crixprof » Qui Out 15, 2009 10:40
- 2 Respostas
- 3157 Exibições
- Última mensagem por crixprof

Sex Out 16, 2009 18:27
Geometria Espacial
-
- Geometria Espacial
por geriane » Sáb Abr 03, 2010 10:39
- 4 Respostas
- 4201 Exibições
- Última mensagem por geriane

Dom Abr 04, 2010 10:29
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) . é so utilizar as formuals de piramides. isso para questao c.
. é so utilizar as formuals de piramides. isso para questao c.

 .
.
 :
: