 por silvia fillet » Sex Fev 17, 2012 14:13
por silvia fillet » Sex Fev 17, 2012 14:13
Uma pirâmide de base pentagonal regular é seccionada por um plano paralelo à sua base e que passa pelos pontos médios de suas arestas, ficando assim determinada uma nova pirâmide pentagonal regular, com altura igual à metade da altura da pirâmide inicial.
a)Determine as áreas das bases das pirâmides inicial e nova e a razão entre estas áreas
b)Determine também a razão entre seus volumes.
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por MarceloFantini » Sex Fev 17, 2012 14:21
por MarceloFantini » Sex Fev 17, 2012 14:21
Quais foram suas tentativas?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Rosana Vieira » Ter Fev 21, 2012 11:22
por Rosana Vieira » Ter Fev 21, 2012 11:22
Bom Marcelo para o item chegei nesta resolução
b) v1/v2 = 1/3.A1.h / 1/3.A1.h/2 = 32 sem^2.36º
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Fev 21, 2012 12:20
por MarceloFantini » Ter Fev 21, 2012 12:20
Sejam
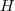
e

as alturas maior e menor respectivamente. Então
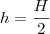
. A razão entre os volumes será o cubo da razão entre os segmentos, logo
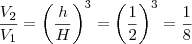
onde
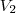
é o volume da pirâmide menor e

da pirâmide original. O raciocínio é análogo para as áreas.
Como você chegou nesta resolução? Porque suas contas não fazem sentido, o valor
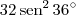
parece quase um chute.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Rosana Vieira » Ter Fev 21, 2012 16:46
por Rosana Vieira » Ter Fev 21, 2012 16:46
MarceloFantini escreveu:Sejam
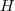
e

as alturas maior e menor respectivamente. Então
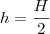
. A razão entre os volumes será o cubo da razão entre os segmentos, logo
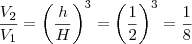
onde
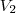
é o volume da pirâmide menor e

da pirâmide original. O raciocínio é análogo para as áreas.
Como você chegou nesta resolução? Porque suas contas não fazem sentido, o valor
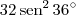
parece quase um chute.
Obrigado Marcelo pela explicação.
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MickaelSantos » Ter Fev 21, 2012 20:20
por MickaelSantos » Ter Fev 21, 2012 20:20
Primeiro eu dividi o pentágono da base em 5 triângulos e, chamando cada lado do pentágono de l, calculei a altura de cada triângulo assim:
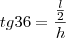
, onde l é o lado do triângulo e h a altura dele.
Desenvolvendo a expressão, cheguei em:

Depois calculei a área do triângulo e multipliquei por 5, que é a quantidade de triângulos do pentágono:
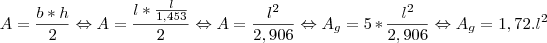
Onde:
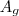
é a área do pentágono da pirâmide maior.
Então eu comparei a medida do lado do pentágono menor com a do pentágono maior, usando o Teorema de Tales:
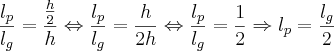
Onde:
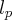
é o lado do pentágono da pirâmide menor e
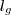
é o lado do pentágono da pirâmide maior
Obs. tenho dúvidas nessa parte!
Agora o cálculo da área do pentágono menor, usando a fórmula acima:
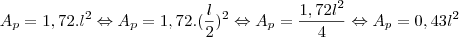
Agora a relação:
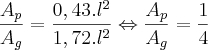
Isso quer dizer que a área do pentágono da pirâmide maior é 4 vezes a área do pentágono da pirâmide menor.
Acho que é isso...
Se alguém puder dar uma olhada e ver se está certo, principalmente na parte da relação entre o lado do maior e o lado do menor, agradeço.
Professor de Matemática
-

MickaelSantos
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Fev 21, 2012 19:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Fev 21, 2012 20:25
por MarceloFantini » Ter Fev 21, 2012 20:25
Sua resposta está certa, mas muito grande e complicada de raciocinar num espaço de tempo curto. Além disso, você aproximou o valor da tangente, apesar que isto não influencia o resultado final.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Rosana Vieira » Ter Fev 21, 2012 20:36
por Rosana Vieira » Ter Fev 21, 2012 20:36
MickaelSantos escreveu:Primeiro eu dividi o pentágono da base em 5 triângulos e, chamando cada lado do pentágono de l, calculei a altura de cada triângulo assim:
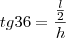
, onde l é o lado do triângulo e h a altura dele.
Desenvolvendo a expressão, cheguei em:

Depois calculei a área do triângulo e multipliquei por 5, que é a quantidade de triângulos do pentágono:
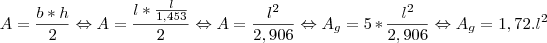
Onde:
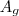
é a área do pentágono da pirâmide maior.
Então eu comparei a medida do lado do pentágono menor com a do pentágono maior, usando o Teorema de Tales:
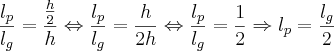
Onde:
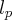
é o lado do pentágono da pirâmide menor e
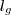
é o lado do pentágono da pirâmide maior
Obs. tenho dúvidas nessa parte!
Agora o cálculo da área do pentágono menor, usando a fórmula acima:
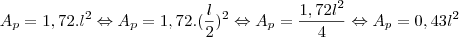
Agora a relação:
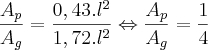
Isso quer dizer que a área do pentágono da pirâmide maior é 4 vezes a área do pentágono da pirâmide menor.
Acho que é isso...
Se alguém puder dar uma olhada e ver se está certo, principalmente na parte da relação entre o lado do maior e o lado do menor, agradeço.
Olá Mickael este exercício é a letra a ou b
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Fev 21, 2012 20:39
por MarceloFantini » Ter Fev 21, 2012 20:39
Rosana, evite citar a resposta inteira, cite apenas as partes que te interessam. Pelo contexto você não percebeu? Olhe as questões e olhe qual razão que encontrou.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MickaelSantos » Ter Fev 21, 2012 20:40
por MickaelSantos » Ter Fev 21, 2012 20:40
Obrigado pela resposta, Marcelo.
Mas será que tem outro jeito de pensar nela?
Será que posso pensar que como o lado do menor é a metade do lado do maior, e que a área varia com o quadrado da distância, e que a área do maior está ao dobro da distância da área do menor (em relação ao vértice), o valor da área do maior é 4 vezes a do menor?
Ufa!!! Precisei fazer do jeito mais complicado para entender o mais fácil. Gostei!
Mas a resposta longa é a mais indicada para uma aula de PÓS, pois mostra que você entende do assunto, certo?
Abr@ço...
Professor de Matemática
-

MickaelSantos
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Fev 21, 2012 19:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MickaelSantos » Ter Fev 21, 2012 20:42
por MickaelSantos » Ter Fev 21, 2012 20:42
Olá Mickael este exercício é a letra a ou b
Exercício 2, item a.
Professor de Matemática
-

MickaelSantos
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Fev 21, 2012 19:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Fev 21, 2012 20:47
por MarceloFantini » Ter Fev 21, 2012 20:47
Se você lembrar do teorema da base média, o raciocínio também é rápido. Em cada face lateral, o lado do pentágono será base média deste, logo cada lado terá metade do valor do lado original. Daí, a área será um quarto da área original. A resposta para o volume segue.
Ser mais longo não necessariamente significa ser bom. Neste caso, muitas saídas rápidas existem sem grandes complicações, pensar no teorema de tales, usar trigonometria e manipulações algébricas longas podem induzir erros devido ao tamanho do processo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MickaelSantos » Ter Fev 21, 2012 21:03
por MickaelSantos » Ter Fev 21, 2012 21:03
Entendi, quanto maiorfor o caminho, maior a probabilidade de erro.
Obrigado pela força.
Professor de Matemática
-

MickaelSantos
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Fev 21, 2012 19:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geoemtria espacial
por silvia fillet » Sex Fev 17, 2012 14:12
- 3 Respostas
- 2557 Exibições
- Última mensagem por MarceloFantini

Ter Fev 21, 2012 21:34
Geometria Espacial
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11733 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2837 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6133 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
-
- Geometria espacial
por crixprof » Qui Out 15, 2009 10:40
- 2 Respostas
- 3147 Exibições
- Última mensagem por crixprof

Sex Out 16, 2009 18:27
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





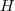 e
e  as alturas maior e menor respectivamente. Então
as alturas maior e menor respectivamente. Então 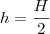 . A razão entre os volumes será o cubo da razão entre os segmentos, logo
. A razão entre os volumes será o cubo da razão entre os segmentos, logo 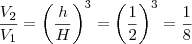 onde
onde 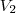 é o volume da pirâmide menor e
é o volume da pirâmide menor e  da pirâmide original. O raciocínio é análogo para as áreas.
da pirâmide original. O raciocínio é análogo para as áreas.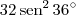 parece quase um chute.
parece quase um chute.

e
as alturas maior e menor respectivamente. Então
. A razão entre os volumes será o cubo da razão entre os segmentos, logo
onde
é o volume da pirâmide menor e
da pirâmide original. O raciocínio é análogo para as áreas.
parece quase um chute.

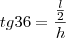 , onde l é o lado do triângulo e h a altura dele.
, onde l é o lado do triângulo e h a altura dele.
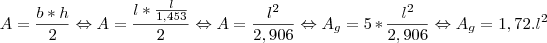
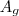 é a área do pentágono da pirâmide maior.
é a área do pentágono da pirâmide maior.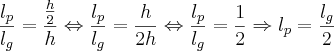
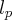 é o lado do pentágono da pirâmide menor e
é o lado do pentágono da pirâmide menor e 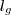 é o lado do pentágono da pirâmide maior
é o lado do pentágono da pirâmide maior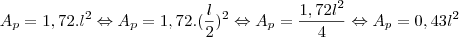
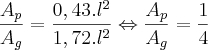



, onde l é o lado do triângulo e h a altura dele.
é a área do pentágono da pirâmide maior.
é o lado do pentágono da pirâmide menor e
é o lado do pentágono da pirâmide maior













