 por gustavoluiss » Seg Jan 09, 2012 21:46
por gustavoluiss » Seg Jan 09, 2012 21:46
Na figura, vista em corte, a esfera de raio r está
colocada no interior do cilindro circular reto de
altura h e cujo raio da base é também igual a r.

O volume interior ao cilindro e exterior à esfera é
igual ao volume da esfera quando:
A) h = 2r
B) h = 7/3 r
C) h = 3r
D) h = 8/3 r
não entendi volume interior ao cilindro e exterior à esfera,
alguém poderia resolver esta questão ?
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por ant_dii » Ter Jan 10, 2012 02:08
por ant_dii » Ter Jan 10, 2012 02:08
Boa noite.
Pra começar
gustavoluiss escreveu:não entendi volume interior ao cilindro e exterior à esfera,
volume interior ao cilindro e exterior à esfera, significa que você tomará somente o volume (o espaço) que sobrou dentro do cilindro sem a esfera, olha tudo mas não conta a esfera.
Para resolver seu problema, primeiro um comentário, seria interessante você colocar o que tentou pra eu poder ver como te ajudar no entendimento. Mas vamos lá:
Primeira coisa vamos dar nomes aos bois, como dizem por aí, façamos
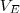
o volume da esfera,

o volume do cilindro e

o volume interior ao cilindro e exterior à esfera. Sabemos que:

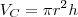
Então, teremos que

.
Agora vamos ver o que o problema pede:
gustavoluiss escreveu:Na figura, vista em corte, a esfera de raio r está
colocada no interior do cilindro circular reto de
altura h e cujo raio da base é também igual a r.

O volume interior ao cilindro e exterior à esfera é
igual ao volume da esfera quando:
A) h = 2r
B) h = 7/3 r
C) h = 3r
D) h = 8/3 r
Então, estamos interessados em saber quando o volume interior ao cilindro e exterior a esfera é igual ao volume da esfera, isto é,
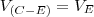
.
Logo,

De onde temos que
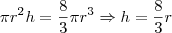
Portanto, a resposta correta é a letra D.
Qualquer dúvida estamos aqui...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- O volume de uma esfera em relação a outra esfera
por Macedo Junior » Sáb Jul 23, 2016 21:01
- 2 Respostas
- 9568 Exibições
- Última mensagem por Macedo Junior

Sáb Jul 23, 2016 23:28
Geometria Plana
-
- cilindro e esfera
por aprendiz » Dom Nov 09, 2008 23:10
- 0 Respostas
- 1292 Exibições
- Última mensagem por aprendiz

Dom Nov 09, 2008 23:10
Geometria Analítica
-
- Cilindro e esfera
por karol-1901 » Qui Out 07, 2010 18:30
- 2 Respostas
- 2114 Exibições
- Última mensagem por karol-1901

Sex Out 08, 2010 14:34
Geometria Espacial
-
- Volume do cilindro e da esfera
por Pri Ferreira » Sex Mai 18, 2012 23:24
- 0 Respostas
- 2305 Exibições
- Última mensagem por Pri Ferreira

Sex Mai 18, 2012 23:24
Geometria Espacial
-
- AREA MAXIMA DE CONE RELACAO COM CILINDRO
por netochaves » Qui Mai 16, 2013 17:09
- 0 Respostas
- 1809 Exibições
- Última mensagem por netochaves

Qui Mai 16, 2013 17:09
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



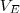 o volume da esfera,
o volume da esfera,  o volume do cilindro e
o volume do cilindro e  o volume interior ao cilindro e exterior à esfera. Sabemos que:
o volume interior ao cilindro e exterior à esfera. Sabemos que:
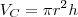
 .
.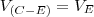 .
.
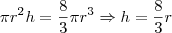


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.