Oi... Gostei muito do site de vcs... de grand eutilidade, sou estudando de engenharia elétrica - UDESC.
Bom, preciso tirar umas duvidas urgentes de algebra I, prciso entender até amanhã...
A dúvida é em relação a 2 questões, que são muito parecidads...
1ª
Encontre as equações reduzidas da reta que passa pelos pontos A(1, 4, -3), B(2, 1, 3) e C(4, -1, 7).
desculpa, ia escrever do jeito que resolvi, mas tah errado e tbm não sei colcar vetores nesse programa ai =(, tentei mas não consegui, então lá vai....
encontrei um vetor diretor AB=v, depois peguei v e o ponto c que pertence a reta, e daí através do vetor diretor da reta e e do ponto c, escreve a equaçao parametrica da reta r....
2ª
Encontre as equaçoes reduzidas da reta que passa pelos pontos A(1, 4, 3), B(2, 1, 3) e C(4, -1, 7) e é perpendicular ao eixo x.
a segunda questão, cheguei a desenhá-la, e percebi que a reta ABC é reversa ao eixo x, como consigo contemplar com elas sendo reversas? se elas forem realmente reversas, deveria somente fazer o produto misto e em seguida, caso elas sejam reversas, falar que não é possivel encontrar tais equaçoes pq a reta pedida é reversa ao eixo x??
muito obrigado...
cara, adorei o site de vcs, muiiiito mesmo!
estou na primeira fase de eng. elétrica, e a partir de hoje, utilizarei quase que diariamente a ajuda de vcs, pq realmente preciso, quanto mais estudamos, mais ignorantes percbemos que somos, aff, isso é triste, portanto... como estudarei muiiito... muitas duvidas surgirção, abraços... obrigado pela ajuda!


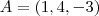 ,
, 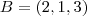 e
e 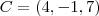
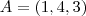 ,
,  real, tal que:
real, tal que: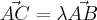
 e
e 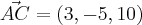 :
:

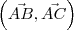 é linearmente independente (LI, portanto, não são paralelos a uma mesma reta).
é linearmente independente (LI, portanto, não são paralelos a uma mesma reta).
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.