 por adauto martins » Sáb Nov 23, 2019 10:15
por adauto martins » Sáb Nov 23, 2019 10:15
(ITA-exame 1953 )
calcular o volume do solido gerado por um triangulo retangulo isosceles,cujos catetos medem 3m,ao girar em torno da paralela
a hipotenusa traçada pelo vertice do angulo reto.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Nov 23, 2019 11:54
por adauto martins » Sáb Nov 23, 2019 11:54
soluçao´
vamos tomar para melhor visualizaçao os eixos´coordenadós,e o vertice do triangulo em questao com o angulo reto na origem,entao teremos o ´triangulo ÁBC,onde A e a origem do sistema x-y...
temos pelio teorama de pelo teoremma de papus
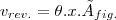
onde

´ angulo de rotaçao ´
x a distancia ´do centro de gravidade(no caso o baricentro do triangulo,ou da fígura plana)

´ que em nosso casso,sera

o problema se resume em achar x...
o x em nosso caso´,sera o baricentro do triangulo(figura),como sabemos o baricentro´(encontro das medianas) fica
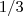
da base e
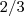
do vertice.em nosso caso o triangulo girara em tórno da paralela a hipotenusa,passando pela origem A do sistema,entao

onde AM´é a mediana que parte da origem A,e divide a hipotenusa áo meio...
como o nosso triang.retanguloé ísosceles,termos
![´h=\sqrt[]{({3}^{2}+{3}^{2})}=3\sqrt[]{2} ´h=\sqrt[]{({3}^{2}+{3}^{2})}=3\sqrt[]{2}](/latexrender/pictures/7568829354a4b6d64239ea6245f2f79e.png)
´
![AM=BD=DC=(1/2)h=(1/2)3.\sqrt[]{2} AM=BD=DC=(1/2)h=(1/2)3.\sqrt[]{2}](/latexrender/pictures/3624c03322b74e4612f56dcd37a720c6.png)
´
pois sendo ABC isosceles,os catetos dos 2 triang. menores teráo mesmo valor,logo
![x=(2/3)AM=(2/3).(1/2)3.\sqrt[]{2}=\sqrt[]{2} x=(2/3)AM=(2/3).(1/2)3.\sqrt[]{2}=\sqrt[]{2}](/latexrender/pictures/d2303e90bd5282b58dfaa73610b6436b.png)
´
portanto
![{v}_{rev.}=\theta.x.A=2.\pi.\sqrt[]{2}.(9/2)=9\pi\sqrt[]{2} {v}_{rev.}=\theta.x.A=2.\pi.\sqrt[]{2}.(9/2)=9\pi\sqrt[]{2}](/latexrender/pictures/e56aec43df9f5214e2de6ee07c134f9e.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exrc.proposto
por adauto martins » Ter Out 08, 2019 20:19
- 0 Respostas
- 4882 Exibições
- Última mensagem por adauto martins

Ter Out 08, 2019 20:19
Trigonometria
-
- exrc.resolv.combinatoria
por adauto martins » Ter Jul 23, 2019 18:14
- 2 Respostas
- 5763 Exibições
- Última mensagem por adauto martins

Qua Jul 24, 2019 15:09
Análise Combinatória
-
- exercicio resolvido
por adauto martins » Sex Jul 15, 2016 14:48
- 0 Respostas
- 33682 Exibições
- Última mensagem por adauto martins

Sex Jul 15, 2016 14:48
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Qua Jul 20, 2016 18:35
- 0 Respostas
- 31769 Exibições
- Última mensagem por adauto martins

Qua Jul 20, 2016 18:35
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Ter Jul 26, 2016 17:43
- 0 Respostas
- 22006 Exibições
- Última mensagem por adauto martins

Ter Jul 26, 2016 17:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



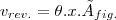
 ´ angulo de rotaçao ´
´ angulo de rotaçao ´ ´ que em nosso casso,sera
´ que em nosso casso,sera
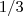 da base e
da base e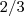 do vertice.em nosso caso o triangulo girara em tórno da paralela a hipotenusa,passando pela origem A do sistema,entao
do vertice.em nosso caso o triangulo girara em tórno da paralela a hipotenusa,passando pela origem A do sistema,entao 
![´h=\sqrt[]{({3}^{2}+{3}^{2})}=3\sqrt[]{2} ´h=\sqrt[]{({3}^{2}+{3}^{2})}=3\sqrt[]{2}](/latexrender/pictures/7568829354a4b6d64239ea6245f2f79e.png) ´
´![AM=BD=DC=(1/2)h=(1/2)3.\sqrt[]{2} AM=BD=DC=(1/2)h=(1/2)3.\sqrt[]{2}](/latexrender/pictures/3624c03322b74e4612f56dcd37a720c6.png) ´
´![x=(2/3)AM=(2/3).(1/2)3.\sqrt[]{2}=\sqrt[]{2} x=(2/3)AM=(2/3).(1/2)3.\sqrt[]{2}=\sqrt[]{2}](/latexrender/pictures/d2303e90bd5282b58dfaa73610b6436b.png) ´
´![{v}_{rev.}=\theta.x.A=2.\pi.\sqrt[]{2}.(9/2)=9\pi\sqrt[]{2} {v}_{rev.}=\theta.x.A=2.\pi.\sqrt[]{2}.(9/2)=9\pi\sqrt[]{2}](/latexrender/pictures/e56aec43df9f5214e2de6ee07c134f9e.png)






