 por adauto martins » Sex Set 27, 2019 16:21
por adauto martins » Sex Set 27, 2019 16:21
(ene-escola nacional de engenharia,rj-exame de admissao )
calcular o volume de um cone de revoluçao cujo raio da base mede 6 m e cuja geratriz e igual a diagonal de um cubo tendo como aresta o lado de um triangulo equilatero inscrito em um circulo de raio igual a 10/3 m.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Dom Out 13, 2019 22:02
por adauto martins » Dom Out 13, 2019 22:02
soluçao:

com os dados de r=6m,devemos encontrar h...
entao:
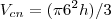
pelos dados,temos:
![{g}_{cn}={d}_{c}=\sqrt[]{3}a {g}_{cn}={d}_{c}=\sqrt[]{3}a](/latexrender/pictures/13fa8602df4955bc937a616f591a9fb9.png)
,
onde a é a aresta do cubo,cujo valor pelos dados sera:
![{g}_{cn}=\sqrt[]{3}a=\sqrt[]{3}(({r}_{c}).\sqrt[]{3})\\
{g}_{cn} =3.(10/3)=10 m {g}_{cn}=\sqrt[]{3}a=\sqrt[]{3}(({r}_{c}).\sqrt[]{3})\\
{g}_{cn} =3.(10/3)=10 m](/latexrender/pictures/8e4bdffa2bb075b395eb6ccdc22bcc68.png)
agora vamos achar o valor de h,do cone que queremos calcular o volume,logo:
![{h}^{2}{{g}_{cn}}^{2}-{r}_{cn}={10}^{2}-{6}^{2}=100-36
h=\sqrt[]{100-36}=8m {h}^{2}{{g}_{cn}}^{2}-{r}_{cn}={10}^{2}-{6}^{2}=100-36
h=\sqrt[]{100-36}=8m](/latexrender/pictures/ce058e8708fa9493ae2e4b7e9baabb8d.png)
portanto:

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 15:41
- 1 Respostas
- 12330 Exibições
- Última mensagem por DanielFerreira

Ter Set 17, 2019 12:53
Equações
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 15:51
- 1 Respostas
- 12624 Exibições
- Última mensagem por DanielFerreira

Ter Set 17, 2019 12:45
Polinômios
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 16:02
- 1 Respostas
- 4911 Exibições
- Última mensagem por adauto martins

Qui Set 19, 2019 09:39
Equações
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 16:09
- 4 Respostas
- 8694 Exibições
- Última mensagem por adauto martins

Sex Out 11, 2019 10:34
Números Complexos
-
- exerc.proposto
por adauto martins » Ter Set 17, 2019 10:30
- 1 Respostas
- 4210 Exibições
- Última mensagem por adauto martins

Seg Set 23, 2019 23:57
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



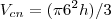
![{g}_{cn}={d}_{c}=\sqrt[]{3}a {g}_{cn}={d}_{c}=\sqrt[]{3}a](/latexrender/pictures/13fa8602df4955bc937a616f591a9fb9.png) ,
,![{g}_{cn}=\sqrt[]{3}a=\sqrt[]{3}(({r}_{c}).\sqrt[]{3})\\
{g}_{cn} =3.(10/3)=10 m {g}_{cn}=\sqrt[]{3}a=\sqrt[]{3}(({r}_{c}).\sqrt[]{3})\\
{g}_{cn} =3.(10/3)=10 m](/latexrender/pictures/8e4bdffa2bb075b395eb6ccdc22bcc68.png)
![{h}^{2}{{g}_{cn}}^{2}-{r}_{cn}={10}^{2}-{6}^{2}=100-36
h=\sqrt[]{100-36}=8m {h}^{2}{{g}_{cn}}^{2}-{r}_{cn}={10}^{2}-{6}^{2}=100-36
h=\sqrt[]{100-36}=8m](/latexrender/pictures/ce058e8708fa9493ae2e4b7e9baabb8d.png)


 .
.



