-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478215 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532247 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495746 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 706875 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2123662 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por rochadapesada » Ter Abr 16, 2013 19:24
por rochadapesada » Ter Abr 16, 2013 19:24
Uma esfera de diâmetro 6 cm está inscrita em um cone de altura 8 cm. Então a área da base do cone vale:
a)
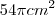
b
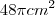
c)
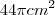
d)
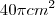
e)
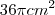
Eu não conseguir desenvolver com esse diâmetro e altura, se o cone fosse equilátero facilitaria, mas como é um cone normal então não sei como começar
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Ter Abr 16, 2013 21:06
por young_jedi » Ter Abr 16, 2013 21:06
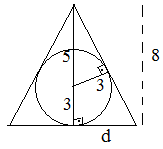
- triangulo.png (2.01 KiB) Exibido 4588 vezes
utilize semelhança de triangulos, nos dois triangulos retangulos e encontre o valor d
que é o raio da base do cone
comente qualquer duvida
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por rochadapesada » Qua Abr 17, 2013 20:27
por rochadapesada » Qua Abr 17, 2013 20:27
Brigadão =D
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Espacial] Volume do tronco do cone
por jukkax » Sáb Out 19, 2013 21:32
- 1 Respostas
- 2959 Exibições
- Última mensagem por young_jedi

Dom Out 20, 2013 22:43
Geometria Espacial
-
- Esfera inscrita em um cubo
por zenildo » Seg Jul 13, 2015 00:16
- 1 Respostas
- 2541 Exibições
- Última mensagem por nakagumahissao

Qui Jul 16, 2015 17:33
Geometria Plana
-
- Esfera e cone
 por Ananda » Sex Abr 04, 2008 15:21
por Ananda » Sex Abr 04, 2008 15:21
- 4 Respostas
- 7860 Exibições
- Última mensagem por admin

Sex Abr 04, 2008 17:49
Geometria Espacial
-
- Questão sobre esfera e cone
 por oeslle » Qui Out 16, 2008 22:42
por oeslle » Qui Out 16, 2008 22:42
- 4 Respostas
- 3867 Exibições
- Última mensagem por oeslle

Sex Out 17, 2008 19:53
Geometria Espacial
-
- Altura do cone inscritível na esfera de raio R
por Luiz 2017 » Sex Set 22, 2017 20:46
- 0 Respostas
- 2726 Exibições
- Última mensagem por Luiz 2017

Sex Set 22, 2017 20:46
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 17 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
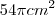
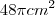
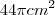
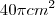
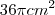

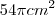
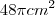
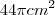
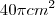
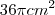





 , avisa que eu resolvo.
, avisa que eu resolvo.

