 por weverton » Qui Set 02, 2010 02:40
por weverton » Qui Set 02, 2010 02:40
um tanque em forma de paralelepipedo tem como base uma região retangular de 30 cm por 20 cm.
ele esta com agua ate o nivel de 7.5 cm,quando um cubo solido é completamente mergulhado no tanque,o nivel da agua se eleva em 0.5 cm.quanto mede, aproximadamante, a aresta do cubo?
desde ja agradeço!
-
weverton
- Usuário Parceiro

-
- Mensagens: 62
- Registrado em: Sex Mai 14, 2010 01:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: enfermagem
- Andamento: formado
 por weverton » Sáb Set 04, 2010 00:44
por weverton » Sáb Set 04, 2010 00:44
olha não bateu com o babarito não!!
a resposta é : 6,7cm
eu queria saber como se chega neste valor!!
se vc poder me ajudar.
-
weverton
- Usuário Parceiro

-
- Mensagens: 62
- Registrado em: Sex Mai 14, 2010 01:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: enfermagem
- Andamento: formado
 por Douglasm » Sáb Set 04, 2010 09:05
por Douglasm » Sáb Set 04, 2010 09:05
Bom Weverton, o que Fantini te deu foi o volume do cubo, para que você finalizasse encontrando a aresta, não faz idéia de como fazê-lo? (Caso a resposta seja negativa, simplesmente procure como se calcula esse volume na internet ou em algum livro, pois é bastante simples.)
Nota: O volume do cubo está de acordo com a resposta pedida.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por weverton » Qua Set 08, 2010 02:43
por weverton » Qua Set 08, 2010 02:43
OLHA VC NAO PODERIA ME AJUDAR?
estou aqui enteresado em aprender e nesta materia estou meio empacado neste exercicio!
se vc poder me ajudar ficarei mto agradecido!
-
weverton
- Usuário Parceiro

-
- Mensagens: 62
- Registrado em: Sex Mai 14, 2010 01:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: enfermagem
- Andamento: formado
 por weverton » Qua Set 08, 2010 02:46
por weverton » Qua Set 08, 2010 02:46
OLHA VC NAO PODERIA ME AJUDAR?
estou aqui enteresado em aprender e nesta materia estou meio empacado neste exercicio!
se vc poder me ajudar ficarei mto agradecido,
ou pelomenos me falar a formula que deverei usar para chegar ao resultado!
-
weverton
- Usuário Parceiro

-
- Mensagens: 62
- Registrado em: Sex Mai 14, 2010 01:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: enfermagem
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- nao consegui fazer me ajudem
por weverton » Sáb Ago 14, 2010 01:58
- 1 Respostas
- 3852 Exibições
- Última mensagem por DanielRJ

Dom Ago 22, 2010 00:43
Estatística
-
- Exercícios que não consegui fazer! Me ajudem?!
por mtuliopaula » Seg Nov 09, 2009 14:46
- 1 Respostas
- 6362 Exibições
- Última mensagem por Neperiano

Dom Set 18, 2011 13:50
Estatística
-
- Média - não consegui fazer
por cidaiesbik » Qui Mai 21, 2009 10:32
- 2 Respostas
- 3216 Exibições
- Última mensagem por cidaiesbik

Seg Mai 25, 2009 10:18
Desafios Enviados
-
- Não consegui fazer, ajuda?
por Loretto » Sáb Nov 20, 2010 02:13
- 3 Respostas
- 2350 Exibições
- Última mensagem por DanielFerreira

Seg Nov 29, 2010 19:27
Sistemas de Equações
-
- duvida não consegui fazer
por Fabricio dalla » Ter Jul 12, 2011 15:19
- 1 Respostas
- 2560 Exibições
- Última mensagem por SidneySantos

Ter Jul 19, 2011 21:34
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


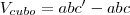 onde
onde 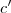 é a altura final e
é a altura final e  a altura inicial.
a altura inicial. 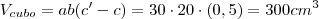



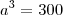
 é a aresta do cubo. Termine.
é a aresta do cubo. Termine.

 , avisa que eu resolvo.
, avisa que eu resolvo.

