 por eliane e rodrigo » Seg Ago 23, 2010 22:33
por eliane e rodrigo » Seg Ago 23, 2010 22:33
Qual o volume do cilindro?
- Anexos
-
[O anexo não pode ser exibido, pois a extensão doc foi desativada pelo administrador.]
-
eliane e rodrigo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Ago 23, 2010 21:40
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Ter Ago 24, 2010 16:38
por Molina » Ter Ago 24, 2010 16:38
eliane e rodrigo escreveu:Qual o volume do cilindro?
Boa tarde.
Sugiro que você primeiramente calcule o volume total do ciclindro, que é dado por
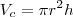
onde

e

são dados no problema.
Posteriormente você irá subtrair desse valor o volume daquela parte que foi retirada, que é dado por

onde

é o ângulo que você está tirando (60º, neste caso) e os outros valores já são conhecidos.
Obs.: Você pode também utilizar esta última forma diretamente. Basta considerar
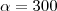
.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por eliane e rodrigo » Ter Ago 24, 2010 16:45
por eliane e rodrigo » Ter Ago 24, 2010 16:45
Gostaria de agradecer, muito obrigada, mesmo
-
eliane e rodrigo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Ago 23, 2010 21:40
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada - calcular a area da figura rotacionada
por maykonnunes » Qui Set 15, 2011 23:54
- 4 Respostas
- 3707 Exibições
- Última mensagem por LuizAquino

Sáb Set 24, 2011 00:39
Cálculo: Limites, Derivadas e Integrais
-
- Calcular lado de uma figura formada por uma recta paralela
por LBT » Dom Dez 05, 2010 17:22
- 2 Respostas
- 1999 Exibições
- Última mensagem por LBT

Seg Dez 06, 2010 05:35
Geometria Analítica
-
- Calcular o volume de uma pirâmide
por -civil- » Qua Jun 15, 2011 21:05
- 2 Respostas
- 2556 Exibições
- Última mensagem por -civil-

Sáb Jun 18, 2011 12:13
Geometria Analítica
-
- [INTEGRAIS DUPLAS]Calcular o volume
por Tathiclau » Sex Jan 10, 2014 01:55
- 2 Respostas
- 3131 Exibições
- Última mensagem por Guilherme Pimentel

Seg Jan 13, 2014 06:24
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] para calcular volume
por neoreload » Sex Nov 21, 2014 05:26
- 1 Respostas
- 4622 Exibições
- Última mensagem por felipederaldino

Qua Nov 26, 2014 11:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



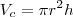
 e
e  são dados no problema.
são dados no problema.
 é o ângulo que você está tirando (60º, neste caso) e os outros valores já são conhecidos.
é o ângulo que você está tirando (60º, neste caso) e os outros valores já são conhecidos.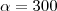 .
.

