A=
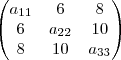
A soma das áreas totais dos três tetraedros, em m², é
a)
![18 \sqrt[]{3} 18 \sqrt[]{3}](/latexrender/pictures/59a3dd778c04962c8509f68377ffe288.png)
b)
![30 \sqrt[]{3} 30 \sqrt[]{3}](/latexrender/pictures/5e9c0a7c15ce60c17aed57e7ab4e74f0.png)
c)
![36 \sqrt[]{3} 36 \sqrt[]{3}](/latexrender/pictures/ba717ca88741b9b6f792685e6bb2d0ba.png)
d)
![84 \sqrt[]{3} 84 \sqrt[]{3}](/latexrender/pictures/ed9c21d56e3687a0e1e4505bec6d3304.png)
Ajuda, por favor!!!

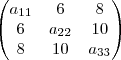
![18 \sqrt[]{3} 18 \sqrt[]{3}](/latexrender/pictures/59a3dd778c04962c8509f68377ffe288.png)
![30 \sqrt[]{3} 30 \sqrt[]{3}](/latexrender/pictures/5e9c0a7c15ce60c17aed57e7ab4e74f0.png)
![36 \sqrt[]{3} 36 \sqrt[]{3}](/latexrender/pictures/ba717ca88741b9b6f792685e6bb2d0ba.png)
![84 \sqrt[]{3} 84 \sqrt[]{3}](/latexrender/pictures/ed9c21d56e3687a0e1e4505bec6d3304.png)

Pri Ferreira escreveu:Considerem-se 3 tetraedros regulares t1,t2 e t3. Cada elemento aij da matriz A3x3, representada abaixo é a soma das medidas em metros da altura do tetraedro tj, com a altura do tetraedro tj
A=
A soma das áreas totais dos três tetraedros, em m², é
a)
b)
c)
d)
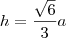
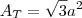
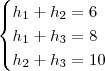

Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: