[Geometria espacial] Prisma hexagonal

por **acargo** » Dom Out 23, 2011 19:13

Olá pessoal.
Estou fazendo uma lista de exercícios de geometria espacial e estou com dificuldade em um deles que já estou há boas horas tentando resolver. Estou muito curiosa então quem puder me ajudar eu agradeço.

O volume de um prisma regular reto hexagonal, com 2 metros de altura, é $\sqrt{3}$ m³. A medida da área lateral deste prisma é ?

Bem, como o volume é dado por AB.h, coloquei $\sqrt{3}=6\frac{x^2\sqrt3}{4}2$ .
Não sei se dá pra achar a resposta assim, então relacionei AB com AL, a qual é 6.x.2=12x, ficou:
$12x=\frac{3x^2\sqrt{3}}{2}$

Mesmo assim a resposta dá absurda, pelo que viram, estou tentando achar aresta primeiro.... Parece tão simples e ao mesmo tempo tão difícil, me expliquem por favor !

por **Adriano Tavares** » Dom Jan 01, 2012 20:39

Olá, acargo.

Como a área da base é formada por seis triângulos equiláteros teremos:

$\sqrt{3}=6.\frac{l^2\sqrt{3}}{4}.2 \Rightarrow \sqrt{3}=3l^2\sqrt{3} \Rightarrow l^2=\frac{1}{3} \Rightarrow l=\frac{\sqrt{3}}{3} \tex{m}$

A área lateral do prisma é formada pois seis retângulos de base

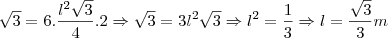
e altura igual a

.

$A_l=6.\frac{\sqrt{3}}{3}.2 \Rightarrow A_l=4\sqrt{3} \tex{m^2}$