cubo

por **camilalindynha** » Ter Dez 11, 2007 18:56

se puder ajudar agradeço

: questao 6 e 10

por **admin** » Ter Dez 11, 2007 20:05

Olá.

Veja a representação da pirâmide citada, com vértices O, E, F, G, H.

: cubo.jpg (22.02 KiB) Exibido 7508 vezes

O volume de uma pirâmide de base quadrada é dado por esta expressão:
$V_{pir}=\frac{1}{3}\cdot L^2 \cdot h$

Novamente, podemos questionar a origem desta expressão.
Podemos obtê-la utilizando o conceito de integrais, posicionando convenientemente a pirâmide no eixo cartesiano e integrando a função área por todas as infinitesimais seções transversais quadradas da pirâmide.

Onde:
área da base da pirâmide (quadrado) = L^2

altura da pirâmide =

Repare que a altura da pirâmide é igual à altura do próprio cubo, que também é igual ao lado do quadrado da base, ou seja:
$V_{pir}=\frac{1}{3}\cdot L^2 \cdot L = \frac{1}{3}\cdot L^3$

Como o volume da pirâmide é dado, temos:
$V_{pir} = 6$

$\frac{1}{3}\cdot L^3 = 6$

$L^3 = 3 \cdot 6$

L^3 = 18

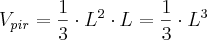
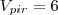
(que é o volume procurado do cubo, em 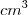cm^3

, alternativa b)

cubo

cubo

cubo

Re: cubo

Quem está online