 por gustavowelp » Qui Nov 25, 2010 09:05
por gustavowelp » Qui Nov 25, 2010 09:05
Caros amigos, pensei na questão mas não entendi muito bem como resolvê-la:
Considere uma tora de madeira de formato cilíndrico cuja circunferência mede 314 cm e cujo comprimento mede 6 metros. Deseja-se serrar essa tora de modo a obter uma viga de madeira de seção quadrada,com o mínimo de perda de madeira. Nesse caso, o volume da viga obtida é de:
A resposta correta é 1,50 m3
Realmente não entendi a questão...
Obrigado!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por alexandre32100 » Ter Nov 30, 2010 23:04
por alexandre32100 » Ter Nov 30, 2010 23:04
-
alexandre32100
-
 por gustavowelp » Qua Dez 01, 2010 06:29
por gustavowelp » Qua Dez 01, 2010 06:29
Muito obrigado pela explicação, só não entendi a fórmula para achar o lado...
Valeu!!!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por 0 kelvin » Qua Dez 01, 2010 14:44
por 0 kelvin » Qua Dez 01, 2010 14:44
Tinha pensado nisso:
360 / 4 = 90
Qual o comprimento de uma corda que liga as extremidades de um arco de 90 graus?
Sabendo que pi é 3,14 e o perímetro é 314, dá pra calcular o raio com a fórmula do perímetro.
Traçando dois raios formando um ângulo de 90 graus, tem-se um triângulo retângulo, com dois catetos de comprimento igual ao raio. A hipotenusa seria o lado do quadrado inscrito na circumferência.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por gustavowelp » Qua Dez 01, 2010 20:48
por gustavowelp » Qua Dez 01, 2010 20:48
Nesse caso não daria para usar a fórmula da diagonal?
d =
![lado \sqrt[]{2} lado \sqrt[]{2}](/latexrender/pictures/eaddc66316e0227d94f465cac1a8e7da.png)
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por 0 kelvin » Qua Dez 01, 2010 21:46
por 0 kelvin » Qua Dez 01, 2010 21:46
A diagonal de um quadrado inscrito numa circumferência é o diâmetro.
- Anexos
-
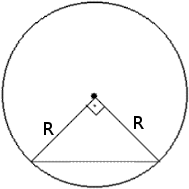
- 90graus.png (5.04 KiB) Exibido 5830 vezes
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por Elcioschin » Qui Dez 02, 2010 16:14
por Elcioschin » Qui Dez 02, 2010 16:14
Resolução aproveitando o desenho do kelvin:
L² = r² + r² ----> L² = 0,5² + 0,5² ----> L² = 0,25 + 0,25 ----> L² = 0,5
Acontece que L² é a área do quadrado da base da tora.
V = Sb*H ----> V = L²*H ----> V = 0,5*3 ----> V = 1,5 m³
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida com KPI da empresa] não sei se é a seção correta
por paulotavaressp » Sex Ago 22, 2014 18:44
- 1 Respostas
- 2120 Exibições
- Última mensagem por paulotavaressp

Sex Ago 22, 2014 18:46
Álgebra Elementar
-
- Dúvida Juros simples' desculpem não encontrei a seção
por deividchou » Qua Ago 12, 2015 11:18
- 1 Respostas
- 4307 Exibições
- Última mensagem por nakagumahissao

Qui Ago 13, 2015 18:04
Estatística
-
- cilindro
por aprendiz » Dom Nov 09, 2008 23:10
- 0 Respostas
- 1300 Exibições
- Última mensagem por aprendiz

Dom Nov 09, 2008 23:10
Geometria Analítica
-
- Cilindro
por geriane » Qui Abr 22, 2010 16:21
- 1 Respostas
- 3422 Exibições
- Última mensagem por MarceloFantini

Qui Abr 22, 2010 17:35
Geometria Espacial
-
- Cilindro.
por nandokmx » Qua Jun 02, 2010 11:40
- 3 Respostas
- 2293 Exibições
- Última mensagem por MarceloFantini

Qui Jun 03, 2010 03:43
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



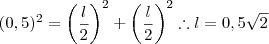
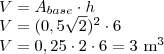
![lado \sqrt[]{2} lado \sqrt[]{2}](/latexrender/pictures/eaddc66316e0227d94f465cac1a8e7da.png)






