Encontre a equação de um plano que passa pelo ponto P = (2,1,0) e é perpendicular aos planos x+2y-3z+2 = 0 e 2x-y+4z=0.r
Então... o problema é que eu não consigo visualizar planos perpendiculares! Com reta tudo bem... mas com planos não. Sei da equação do plano, sei do vetor a..''normal'' ao plano... sei que a interseçao deles é uma reta... mas não consigo encaixar tudo isso para resolvero exercício. Grato a quem puder ajudar !


 , que no qual já foi dado um ponto pertencente a ele, você precisa achar o vetor normal a ele. Sabendo que há 2 planos perpendiculares a ele, n1(vetor normal ao plano1) e n2(vetor normal ao plano2), conclui-se que n1 e n2 são paralelos ao plano
, que no qual já foi dado um ponto pertencente a ele, você precisa achar o vetor normal a ele. Sabendo que há 2 planos perpendiculares a ele, n1(vetor normal ao plano1) e n2(vetor normal ao plano2), conclui-se que n1 e n2 são paralelos ao plano 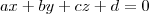 , achar o valor de d e você encontrou a equação geral do plano.
, achar o valor de d e você encontrou a equação geral do plano. , então
, então  e
e  . Em termos de produto interno, que é a caracterização usual, temos
. Em termos de produto interno, que é a caracterização usual, temos 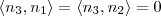 .
. da equação geral do plano
da equação geral do plano  .
.


 .
.
 :
: