Danilo escreveu:Decomponha W = (-1,-3,2) como a soma de dois vetores W1 e W2, com W1 paralelo ao vetor (0,1,3) e W2 ortogonal a este último.
Bom, me deram a sugestão de usar a projeção para resolver...
Bom, sei que W1 = x(0,1,3) x real. e sei que W2 escalar (0,1,3) = 0 Mas não consigo aplicar essas informações para resolver.... Grato a quem puder dar uma luz!
Como você mesmo percebeu, temos que
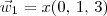
, com x um número real.
Calcule então a projeção de
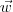
em
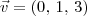
. Escolha chamar essa projeção de
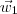
. Note que essa escolha é condizente com os dados do exercício, pois a projeção de
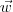
em

é paralelo a

.
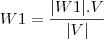
Em seguida, determine
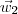
através da relação:
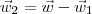
Para entender esse desenvolvimento, vide a figura abaixo.
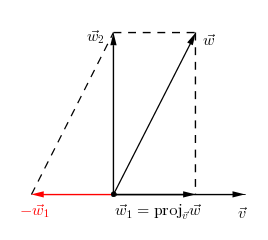
- figura.png (4.18 KiB) Exibido 7522 vezes


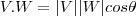
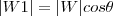
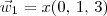 , com x um número real.
, com x um número real.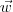 em
em 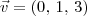 . Escolha chamar essa projeção de
. Escolha chamar essa projeção de 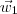 . Note que essa escolha é condizente com os dados do exercício, pois a projeção de
. Note que essa escolha é condizente com os dados do exercício, pois a projeção de  é paralelo a
é paralelo a 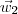 através da relação:
através da relação: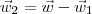

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)