por flaaacs » Qua Out 03, 2012 16:01
por flaaacs » Qua Out 03, 2012 16:01
Seja P um ponto de abscissa positiva, o ponto de intersecção entre a circunferência de equação x^2 +y^2 -2x -2y -7=0 e a reta de equação y-x-3=0. A distância entre o ponto P e a bissetriz dos quadrantes pares é:
Resposta oficial: 5V2/2
(Cinco raiz de dois sobre dois)
-
flaaacs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Out 03, 2012 15:58
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qua Out 03, 2012 17:01
por LuizAquino » Qua Out 03, 2012 17:01
flaaacs escreveu:Seja P um ponto de abscissa positiva, o ponto de intersecção entre a circunferência de equação x^2 +y^2 -2x -2y -7=0 e a reta de equação y-x-3=0. A distância entre o ponto P e a bissetriz dos quadrantes pares é:
Resposta oficial: 5V2/2
(Cinco raiz de dois sobre dois)
Para determinar a interseção entre a circunferência e a reta, você precisa resolver o sistema:

Após resolver esse sistema (por exemplo, por substituição), você irá determinar dois pontos de interseção. O ponto P será aquele que tiver abscissa positiva (ou seja, coordenada x positiva).
Em seguida, você precisa calcular a distância do ponto P até a reta que contém a bissetriz dos quadrantes pares. A equação dessa reta é dada por y = -x (ou seja, x + y = 0). Para calcular essa distância, lembre-se do seguinte: se você tem o ponto

e a reta

, então a distância entre P e r (que aqui vamos representar por d(P, r)), será dada pela fórmula:
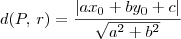
Agora tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Distancia entre ponto e plano
por teneral » Seg Jul 09, 2018 11:29
- 0 Respostas
- 5361 Exibições
- Última mensagem por teneral

Seg Jul 09, 2018 11:29
Geometria Analítica
-
- [distancia entre ponto e reta]
por palomaktk » Seg Jun 03, 2013 00:47
- 0 Respostas
- 4487 Exibições
- Última mensagem por palomaktk

Seg Jun 03, 2013 00:47
Geometria Analítica
-
- [distância entre ponto e reta]
por barbosa-larissa » Seg Jul 08, 2013 21:26
- 1 Respostas
- 2236 Exibições
- Última mensagem por timoteo

Ter Jul 09, 2013 12:05
Geometria Analítica
-
- Distância entre ponto e "curva"
por OtavioBonassi » Sáb Jul 16, 2011 17:59
- 1 Respostas
- 4513 Exibições
- Última mensagem por LuizAquino

Sáb Jul 16, 2011 18:42
Geometria Analítica
-
- [Vetores] Ponto de reta próximo a outros pares de ponto
por cmcrz97 » Ter Jun 19, 2018 20:29
- 0 Respostas
- 2908 Exibições
- Última mensagem por cmcrz97

Ter Jun 19, 2018 20:29
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e a reta
e a reta  , então a distância entre P e r (que aqui vamos representar por d(P, r)), será dada pela fórmula:
, então a distância entre P e r (que aqui vamos representar por d(P, r)), será dada pela fórmula: