 por iarapassos » Sáb Set 01, 2012 22:07
por iarapassos » Sáb Set 01, 2012 22:07
Considere a reta s o ponto Q e o plano a seguir:
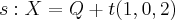
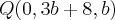
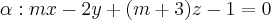
Determine b e m, de modo que a reta s seja paralela ao plano alpha.
Se a reta s é paralela a alpha, logo:
o vetor diretor de s é ortogonal ao vetor normal de alpha.
v.n=0.
Temos que v=(1,0,2) e n=(m,-2,m+3)
Como (1,0,2).(m,-2,m+3)=0
calculando, temos m=-2.
Massa! E como faço agora para achar b?
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Sáb Set 01, 2012 23:57
por LuizAquino » Sáb Set 01, 2012 23:57
iarapassos escreveu:Considere a reta s o ponto Q e o plano a seguir:
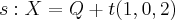
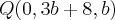
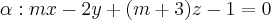
Determine b e m, de modo que a reta s seja paralela ao plano alpha.
Se a reta s é paralela a alpha, logo:
o vetor diretor de s é ortogonal ao vetor normal de alpha.
v.n=0.
Temos que v=(1,0,2) e n=(m,-2,m+3)
Como (1,0,2).(m,-2,m+3)=0
calculando, temos m=-2.
Massa! E como faço agora para achar b?
Bem, quando uma reta é paralela a um plano temos dois casos: a reta não está contida no plano; a reta está contida no plano;
Alguns autores excluem o caso da reta está contida no plano como sendo um caso particular de reta paralela a um plano.
Se esse for o caso do material onde você tirou esse exercício, então nenhum ponto da reta r pode estar no plano

. Desse modo, o ponto Q não pode pertencer ao plano. Tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações de plano] encontrar a equação de um plano
por GHT1810 » Ter Jul 03, 2018 19:42
- 0 Respostas
- 5356 Exibições
- Última mensagem por GHT1810

Ter Jul 03, 2018 19:42
Geometria Analítica
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14950 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
-
- [Equação do Plano Tangente - Plano Paralalelo]
por raimundoocjr » Qui Out 24, 2013 22:10
- 0 Respostas
- 2938 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- Plano
por Rhyu » Dom Abr 08, 2012 10:57
- 2 Respostas
- 1979 Exibições
- Última mensagem por MarceloFantini

Seg Abr 09, 2012 03:40
Geometria Analítica
-
- Plano
por Claudin » Sex Jul 06, 2012 12:32
- 2 Respostas
- 1804 Exibições
- Última mensagem por Claudin

Sex Jul 06, 2012 16:23
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
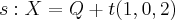
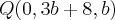
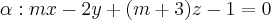


 . Desse modo, o ponto Q não pode pertencer ao plano. Tente continuar a partir daí.
. Desse modo, o ponto Q não pode pertencer ao plano. Tente continuar a partir daí.