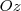 , contendo os pontos
, contendo os pontos 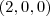 e
e 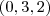
Como iniciar?
O que tem que ser feito seria o cálculo do vetor entre os dois pontos, e depois jogar no sistema com x=0?
Mesmo assim não obtive resultado. Qualquer dica já ajuda

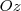 , contendo os pontos
, contendo os pontos 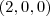 e
e 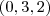

Claudin escreveu:Determine a equação do plano paralelo a, contendo os pontos
e
Como iniciar?
O que tem que ser feito seria o cálculo do vetor entre os dois pontos, e depois jogar no sistema com x=0?
Mesmo assim não obtive resultado. Qualquer dica já ajuda
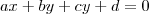
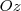 , ou paralelo ao eixo
, ou paralelo ao eixo  , temos
, temos  , com isso
, com isso 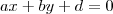
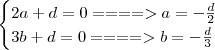
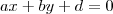
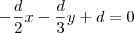

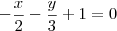
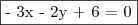

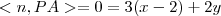
 .
.

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

