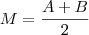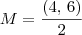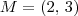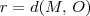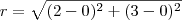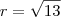por juliacajango » Qua Jun 13, 2012 17:17
por juliacajango » Qua Jun 13, 2012 17:17
oi pessoal, acabei de me registrar; tenho uma duvida em um exercicio da vunesp de domingo agora, dia 10/06/12, o enunciado diz :
Sabe-se que M, ponto médio do segmento AB, é centro de uma
circunferência que passa pela origem (0,0). Sendo A(–1,4) e
B(5,2), conclui-se que o raio dessa circunferência é igual a
tentei esboçar a figura, porém os pontos A e B não passam pelo centro no meu desenho, por favor, alguém sabe resolver este exercicio ?! obrigada...
-
juliacajango
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 13, 2012 17:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino medio
- Andamento: cursando
 por LuizAquino » Qua Jun 13, 2012 20:15
por LuizAquino » Qua Jun 13, 2012 20:15
juliacajango escreveu:oi pessoal, acabei de me registrar; tenho uma duvida em um exercicio da vunesp de domingo agora, dia 10/06/12, o enunciado diz :
Sabe-se que M, ponto médio do segmento AB, é centro de uma
circunferência que passa pela origem (0,0). Sendo A(–1,4) e
B(5,2), conclui-se que o raio dessa circunferência é igual a
tentei esboçar a figura, porém os pontos A e B não passam pelo centro no meu desenho, por favor, alguém sabe resolver este exercicio ?!
Como M é o ponto médio de AB, temos que:
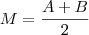

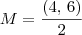
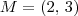
Como M é o centro da circunferência e O = (0, 0) é um ponto dessa circunferência, temos que o seu raio é equivalente a distância entre M e O. Temos então que:
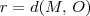
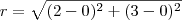
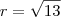
A figura abaixo ilustra o exercício.

- figura.png (11.78 KiB) Exibido 2631 vezes
Perceba que os pontos A e B ficarão dentro da circunferência. Isso irá acontecer pois o comprimento de AB é menor do que o diâmetro da circunferência. Confira isso! Calcule a distância entre A e B e você perceberá que ela é menor do que 2r.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão VUNESP
por LuRodrigues » Seg Abr 23, 2012 13:37
- 1 Respostas
- 10571 Exibições
- Última mensagem por Cleyson007

Seg Abr 23, 2012 16:35
Probabilidade
-
- Questão de concurso da vunesp
por monteyrogab » Sex Mai 01, 2015 13:54
- 0 Respostas
- 1709 Exibições
- Última mensagem por monteyrogab

Sex Mai 01, 2015 13:54
Álgebra Elementar
-
- Dúvida Vunesp
por Vanessa_Dias » Sex Abr 15, 2011 23:49
- 6 Respostas
- 13086 Exibições
- Última mensagem por MarceloFantini

Dom Abr 17, 2011 16:48
Funções
-
- VUNESP
por DanielFerreira » Seg Fev 28, 2011 09:49
- 2 Respostas
- 8258 Exibições
- Última mensagem por DanielFerreira

Seg Fev 28, 2011 11:01
Progressões
-
- ( Vunesp )
por my2009 » Sex Jul 29, 2011 12:18
- 1 Respostas
- 1069 Exibições
- Última mensagem por Molina

Sex Jul 29, 2011 16:21
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.