


CarolMarques escreveu:A equação 7x²+24xy-256x-192y+1456=0 é uma hipérbole que por meio de rotação e translação eu cheguei numa equação reduzida x²/9-y²/16=1 o centro é C(8,6) e o angulo de rotação é o arc sen =3/5 (sen a =3/5 e cos a =4/5).
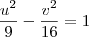
CarolMarques escreveu:Eu não sei achar as assintotas dessa hipérbole.
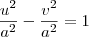 , então as assíntotas dessa hipérbole são
, então as assíntotas dessa hipérbole são 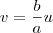 e
e  .
.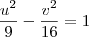 são dadas por
são dadas por  e
e  .
.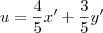 e
e  . Isso nos leva do sistema uOv para o sistema x'O'y'. Temos então que:
. Isso nos leva do sistema uOv para o sistema x'O'y'. Temos então que: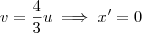
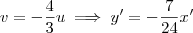
 e
e 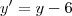 . Isso nos leva do sistema x'O'y' para o sistema xOy. Temos então que:
. Isso nos leva do sistema x'O'y' para o sistema xOy. Temos então que:
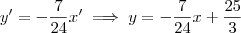
 e
e 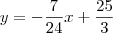 .
.
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.