marinalcd escreveu:Determine as equações da reta que contém a bissetriz do ângulo POQ,
com P = (0; 1;-2), Q = (1; 2; 3) e O = (1;-2; 0).
marinalcd escreveu:Bom, como a reta contém a bissetriz, disse que o ponto O pertence à reta.
Ok.
marinalcd escreveu:Mas não estou conseguindo calcular o vetor, tentei calcular o vetor PQ (que seria um vetor normal à esta reta), mas não estou sabendo transformar este vetor em vetor direção da reta.
Não necessariamente
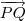
é normal a reta. Isso aconteceria caso o triângulo POQ fosse isósceles, com base PQ. Entretanto, esse não é o caso.
Façamos o seguinte. A partir do triângulo POQ vamos construir o triângulo isósceles P'OQ' tal que PÔQ = P'ÔQ'. Vide a figura abaixo.
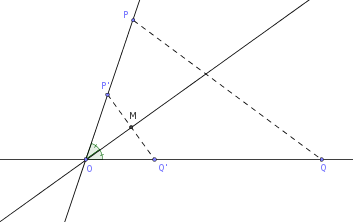
- figura1.png (5.22 KiB) Exibido 682 vezes
A vantagem nessa construção é que a reta que contém a bissetriz irá passar pelo ponto O e pelo ponto M, que é o ponto médio de P'Q' (já que P'OQ' será isósceles).
Desse modo, o nosso primeiro trabalho será determinar P' e Q'.
Por praticidade, vamos determinar P' e Q' tais que
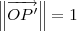
e
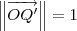
. Para que isso aconteça, basta fazer:
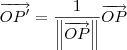
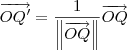
Vamos começar determinando P'. Como
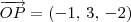
, temos que:
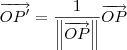
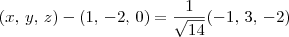
Resolvendo essa equação encontramos que
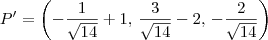
.
Lembrando que
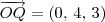
e procedendo de modo análogo, podemos determinar que
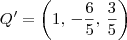
.
Agora tente terminar o exercício a partir daí.


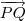 é normal a reta. Isso aconteceria caso o triângulo POQ fosse isósceles, com base PQ. Entretanto, esse não é o caso.
é normal a reta. Isso aconteceria caso o triângulo POQ fosse isósceles, com base PQ. Entretanto, esse não é o caso.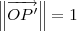 e
e 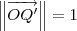 . Para que isso aconteça, basta fazer:
. Para que isso aconteça, basta fazer: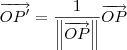
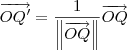
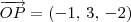 , temos que:
, temos que: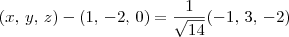
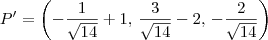 .
.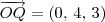 e procedendo de modo análogo, podemos determinar que
e procedendo de modo análogo, podemos determinar que 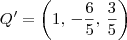 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.