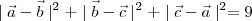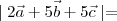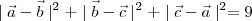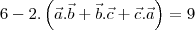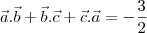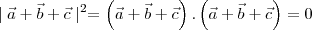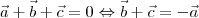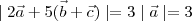por stuart clark » Seg Abr 09, 2012 12:16
por stuart clark » Seg Abr 09, 2012 12:16
If
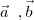
and
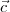
are three vectors such that
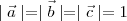
and
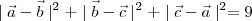
then
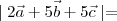
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por stuart clark » Seg Abr 09, 2012 12:19
por stuart clark » Seg Abr 09, 2012 12:19
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por stuart clark » Qua Abr 11, 2012 23:44
por stuart clark » Qua Abr 11, 2012 23:44
Thanks Moderator Got it
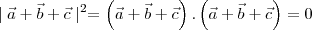
So
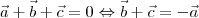
So
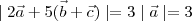
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qui Abr 12, 2012 11:13
por LuizAquino » Qui Abr 12, 2012 11:13
stuart clark escreveu:Thanks Moderator Got it
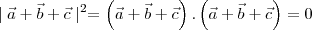
So
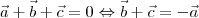
So
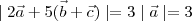
Ok.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
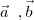 and
and 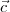 are three vectors such that
are three vectors such that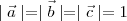 and
and 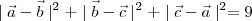
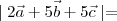

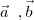 and
and 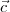 are three vectors such that
are three vectors such that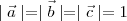 and
and