 por Lucas Ponte » Qui Nov 03, 2011 15:56
por Lucas Ponte » Qui Nov 03, 2011 15:56
Não sei se ta na área certa, não sei se to postando nem no fórum certo. '-'
PS: Sou aluno, não achei nada aqui em relação à aluno e não encontrei outro site qual aparenta ter membros experientes..
Enfim.. Estou com um ângulo aqui que não consigo identificado o valor de "alfa", o qual meu professor
ainda não explicou e provavelmente irá passar de novo uma questão do tipo, já que ninguém conseguiu resolver
Já tentei diversas coisas, como multiplicar em X, somar lado com lado e saber resultado de x ou y..
não me restam mais alternativas para resolver isso, só se eu inventar uma. -rs
A questão seria, qual o valor que alfa assume na representação?

Se bugar:
http://i.imgur.com/VCLEB.jpgAlguém pode ajudar? Agradeço.
-
Lucas Ponte
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Nov 03, 2011 15:39
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Geometria?
- Andamento: cursando
 por LuizAquino » Dom Nov 06, 2011 18:57
por LuizAquino » Dom Nov 06, 2011 18:57
Lucas Ponte escreveu:Qual o valor que alfa assume na representação?
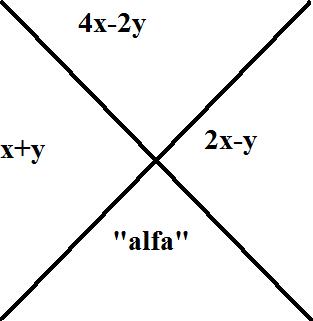
- VCLEB.jpg (10.5 KiB) Exibido 1095 vezes
Os ângulos x + y e 4x - 2y são suplementares. Sendo assim, note que:
(x + y) + (4x - 2y) = 180°
Já os ângulos x + y e 2x - y são opostos pelo vértice. Sendo assim, note que:
x + y = 2x - y
Com essas duas equações, você pode montar o sistema:
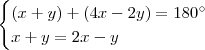
Resolvendo esse sistema, você obtém x = 40° e y = 20°.
Agora note que os ângulos

e 4x - 2y são opostos pelo vértice. Sendo assim, temos que:
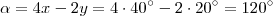
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Plana (soma dos 4 angulos)
 por Rafael Pitzer » Seg Fev 11, 2013 18:54
por Rafael Pitzer » Seg Fev 11, 2013 18:54
- 4 Respostas
- 2045 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 17:02
Geometria Plana
-
- [Questão geometria plana relacionada aos ângulos notáveis]
 por Anniemf » Qua Mar 28, 2012 14:33
por Anniemf » Qua Mar 28, 2012 14:33
- 1 Respostas
- 3552 Exibições
- Última mensagem por kelvinJhonson

Sáb Abr 21, 2012 23:20
Geometria Plana
-
- Ângulos
 por admin » Sex Set 07, 2007 06:42
por admin » Sex Set 07, 2007 06:42
- 3 Respostas
- 13551 Exibições
- Última mensagem por Numwantida

Qui Mai 24, 2018 05:06
Pérolas
-
- Angulos ??????
por ByRobert » Qui Set 01, 2011 12:59
- 6 Respostas
- 9028 Exibições
- Última mensagem por LuizAquino

Qui Set 01, 2011 21:24
Trigonometria
-
- ângulos
 por Thays » Sáb Jan 14, 2012 11:59
por Thays » Sáb Jan 14, 2012 11:59
- 6 Respostas
- 4611 Exibições
- Última mensagem por Thays

Qui Jan 19, 2012 09:36
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



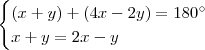
 e 4x - 2y são opostos pelo vértice. Sendo assim, temos que:
e 4x - 2y são opostos pelo vértice. Sendo assim, temos que: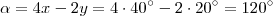 .
.





