o problema é essa seguinte questão:
Achar as equações paramétricas de acordo com a figura:

De:
A e B
C e D
A e D
B e C
D e E
B e D
Daí achei os pontos A(2,0,4) B(0,0,4) C(0,3,0) D(2,3,0) E(2,0,0)
para encontrar a equação paramétrica eu fiz o seguinte
A-B = (2,0,4)-(0,0,4) = (2,0,0)
Eq. paramétrica de A e B-> X= 2+2t// Y=0 Z=4
C-D= (0,3,0)-(2,3,0)= (-2,0,0)
Eq paramétrica de C e D -> X= -2t // Y= 3 // Z= 0 ==> Só que no gabarito o valor de X é igual a 2t
A-D= (2,0,4)-(2,3,0) = (0,-3,4)
Eq paramétrica de C e D-> X= 2// Y= -3t // Z= 4+4t ===> Só que no gabarito o valor de Y = 3t e Z=4-4t.
Resumindo... Nessa questão, estou fazendo o seguinte método: Subtraio o primeiro ponto pelo segundo e depois jogo na fórmula da paramétrica, acontece que o resultado só bate certo se tiver o ponto B, caso contrário tenho que inverter, subtrair o segundo com o primeiro ponto, para o resultado dar igual ao gabarito.
A minha dúvida é essa..
Espero que tenham entendido.
http://imageshack.us/photo/my-images/58 ... log33.jpg/ o link da figura que tem na questão.
desde já obrigado.


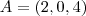
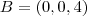
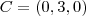


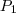 e
e 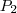 por
por  para
para ![t \in [0,1] t \in [0,1]](/latexrender/pictures/dff6e05ec00b53d46e366975136d0d2e.png) . Quando
. Quando  , temos
, temos  e para
e para  temos
temos  . Assim, parametrizando alguns:
. Assim, parametrizando alguns:

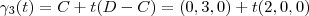


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
