380625 escreveu:Por que quando vamos estudar produtos escalares e é considerado um sistema de coordenadas a formula esta sem o cos teta. . No livro do Boulos ele friza bem que se os vetores pertencem a uma base ortonormal o produto escalar é dado por u*v= x1y1 + x2y2 + x3y3
E pq na outra formula tem a informação que o produto escalar so depende do comprimento dos vetores e dos angulos entre eles. u*v= ||u|| . ||v|| cos teta.
Vamos estudar
com atenção o que está escrito no livro de Boulos (Geometria Analítica - um tratamento vetorial).
Ele primeiro
define o que vem a ser ângulo entre vetores. Em seguida, ele quer determinar uma fórmula para calcular esse ângulo.
Ele toma então os vetores não nulos

e

escritos em uma base ortonormal. A escolha da base ortonormal é importante, pois facilita o cálculo do módulo dos vetores.
Aplicando a
Lei dos Cossenos , ele obtém a seguinte equação:
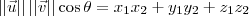
Com essa equação ele obteve uma maneira de calcular o cosseno do ângulo entre os vetores. Basta dividir toda a equação por

(o que poderá ser feito pois os vetores não são nulos):

A partir de agora ele decide
definir uma nova operação entre vetores, chamada de produto escalar:

Acontece que com essa definição escolhida por ele, considerando a equação anterior obtida através da Lei dos Cossenos, o produto escalar
também pode ser escrito como:

Entretanto, o produto escalar só pode ser escrito dessa forma caso a base escolhida seja ortonormal. Caso contrário, a equação obtida através da Lei dos Cossenos seria outra e portanto a fórmula para o produto escalar também mudaria.


 e
e  escritos em uma base ortonormal. A escolha da base ortonormal é importante, pois facilita o cálculo do módulo dos vetores.
escritos em uma base ortonormal. A escolha da base ortonormal é importante, pois facilita o cálculo do módulo dos vetores.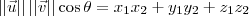
 (o que poderá ser feito pois os vetores não são nulos):
(o que poderá ser feito pois os vetores não são nulos):



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
