Fiquei na dúvida se postava aqui em G.A. ou em Cálculo... Enfim!
O problema é o seguinte:
Determine a área da região englobada pelo laço interno da limaçon:
[Sugestão: r < ou = 1 sobre o intervalo de integração.]
Pois bem. Percebe-se que a limaçon em questão tem um laço visto que 1/b = 1/2 = 0,5.
Da mesma maneira, a está deitada para a esquerda (equação cosseno e positiva).
Pensando na simetria, achei que a equação fica zerada quando:
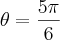ou 
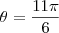
Mas usando os limites de integração
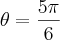ou 
o resultado não bate. De acordo com o solucionário, o limite de integração seria:
e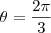 
Ele multiplicou a integral por 2, visto que usou simetria.
Alguém pode me explicar estes limites?
Resposta da integral:
![\theta = \pi - \frac{3\sqrt[]{3}}{2}](/latexrender/pictures/6a0c1027fb7adca080d3d1ce0d4c6025.png "\theta = \pi - \frac{3\sqrt[]{3}}{2}")
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)