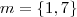por CloudP4 » Qui Jul 01, 2010 22:56
por CloudP4 » Qui Jul 01, 2010 22:56
Boa noite, bem, não conseguir de jeito nenhum resolver esse exercício, todas as maneiras que tentei não consigo chegar ao resultado. É um exercício do livro do Paulo Winterle, Vetores e Geometria Analítica, Pag. 143, exercício 33, segue abaixo:
Determinar o valor de m para que seja de 30º o ângulo entre os planos
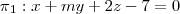
e
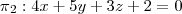
Ok, faço certinho, obtenho os 2 pontos e jogo na fórmula:
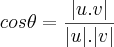
Porém de jeito nenhum chego a resposta, que é segundo o gabarito do livro, 1 ou 7
Alguém poderia ajudar?
Abraços.
-
CloudP4
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 07, 2010 23:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por Tom » Sex Jul 02, 2010 04:24
por Tom » Sex Jul 02, 2010 04:24
Fantini escreveu: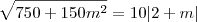
Continuando:
Com Domínio em

,

é sempre não-nulo, assim:
i)Para

, temos:
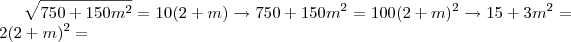
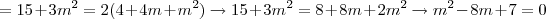
cujas raízes são:

e
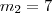
, ambas compreendidas na condição de contorno do intervalo.
ii) Para
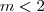
, temos:
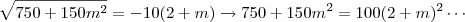
que conduzirá às mesmas raízes do caso anterior, mas estas estarão, agora, fora do intervalo definido.
Assim, os valores que

pode assumir são:
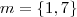
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por MarceloFantini » Sex Jul 02, 2010 15:29
por MarceloFantini » Sex Jul 02, 2010 15:29
Nossa, que cagada que eu fiz. Não sei de onde tirei
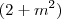
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ângulo entre reta e plano
por manuoliveira » Ter Mai 22, 2012 22:42
- 1 Respostas
- 2709 Exibições
- Última mensagem por LuizAquino

Qua Mai 23, 2012 20:16
Geometria Analítica
-
- [Ângulo - reta e plano] Dúvida exercício
por MrJuniorFerr » Sex Out 12, 2012 11:51
- 6 Respostas
- 4608 Exibições
- Última mensagem por MarceloFantini

Sex Out 12, 2012 20:18
Geometria Analítica
-
- [Ângulo/circunferência] Ângulo CÂB, ajude-me!
 por miltonsermoud » Qua Set 30, 2015 17:14
por miltonsermoud » Qua Set 30, 2015 17:14
- 3 Respostas
- 3503 Exibições
- Última mensagem por miltonsermoud

Sex Out 02, 2015 07:41
Geometria Plana
-
- [Equações de plano] encontrar a equação de um plano
por GHT1810 » Ter Jul 03, 2018 19:42
- 0 Respostas
- 5361 Exibições
- Última mensagem por GHT1810

Ter Jul 03, 2018 19:42
Geometria Analítica
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14956 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
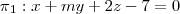
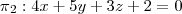
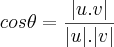

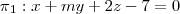
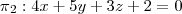
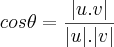


 ,
,  é sempre não-nulo, assim:
é sempre não-nulo, assim: , temos:
, temos: 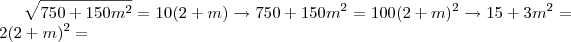
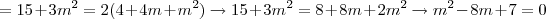 cujas raízes são:
cujas raízes são:  e
e 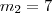 , ambas compreendidas na condição de contorno do intervalo.
, ambas compreendidas na condição de contorno do intervalo.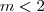 , temos:
, temos: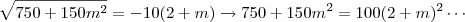 que conduzirá às mesmas raízes do caso anterior, mas estas estarão, agora, fora do intervalo definido.
que conduzirá às mesmas raízes do caso anterior, mas estas estarão, agora, fora do intervalo definido. pode assumir são:
pode assumir são: