-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478186 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 531946 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495477 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 706096 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2122275 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por isabellasimao » Sáb Abr 11, 2020 15:37
por isabellasimao » Sáb Abr 11, 2020 15:37
Oii gente, primeira vez no fórum então me desculpem qualquer coisa, a questão é a seguinte:
Encontre um vetor unitário que seja ortogonal ao plano que passa pelos pontos A(1,1,0), B(1,0,1) e C(0,1,1).
O problema é que eu não sei nem por onde começar, eu sei fazer um vetor ortogonal que passa por esses pontos, mas eu não sei o que seria um "vetor unitário" e o que isso muda na resolução, se alguém puder me ajudar eu ficaria grata.
-
isabellasimao
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 29, 2020 16:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia
- Andamento: cursando
 por adauto martins » Dom Abr 12, 2020 19:33
por adauto martins » Dom Abr 12, 2020 19:33
vamos tomar os vetores
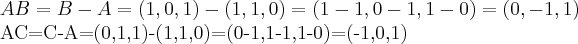
AB e AC,teem que ser linearmente independentes(LI)
para verificar tal condiçao,teriamos que ter

fica como exercicio...
entao suporemos AB,AC (LI)
o produto vetorial AB X AC é perpendicular(ortogonal) ao plano gerado por AB,AC
logo,vamos tomar
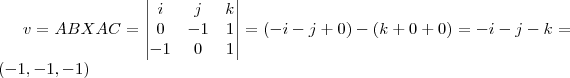
o unitario de v é
![{u}_{v}=(v/\left|v \right|)
\left|v \right|=\sqrt[]{(-1)^2+(-1)^2+(-1)^2}=\sqrt[]{3}
{u}_{v}=(-1/\sqrt[]{3},-1/\sqrt[]{3},-1/\sqrt[]{3}) {u}_{v}=(v/\left|v \right|)
\left|v \right|=\sqrt[]{(-1)^2+(-1)^2+(-1)^2}=\sqrt[]{3}
{u}_{v}=(-1/\sqrt[]{3},-1/\sqrt[]{3},-1/\sqrt[]{3})](/latexrender/pictures/8a0b1982884a18a22a9b88a180f1d008.png)
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por isabellasimao » Qua Abr 15, 2020 15:14
por isabellasimao » Qua Abr 15, 2020 15:14
adauto martins escreveu:vamos tomar os vetores
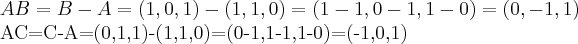
AB e AC,teem que ser linearmente independentes(LI)
para verificar tal condiçao,teriamos que ter

fica como exercicio...
entao suporemos AB,AC (LI)
o produto vetorial AB X AC é perpendicular(ortogonal) ao plano gerado por AB,AC
logo,vamos tomar
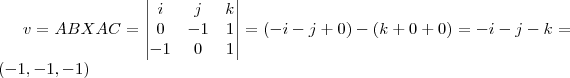
o unitario de v é
![{u}_{v}=(v/\left|v \right|)
\left|v \right|=\sqrt[]{(-1)^2+(-1)^2+(-1)^2}=\sqrt[]{3}
{u}_{v}=(-1/\sqrt[]{3},-1/\sqrt[]{3},-1/\sqrt[]{3}) {u}_{v}=(v/\left|v \right|)
\left|v \right|=\sqrt[]{(-1)^2+(-1)^2+(-1)^2}=\sqrt[]{3}
{u}_{v}=(-1/\sqrt[]{3},-1/\sqrt[]{3},-1/\sqrt[]{3})](/latexrender/pictures/8a0b1982884a18a22a9b88a180f1d008.png)
...
Obrigada, sua explicação foi muito esclarecedora!!
-
isabellasimao
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 29, 2020 16:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Analitica Vetor Unitario
por Diego Silva » Sáb Jul 20, 2013 12:14
- 6 Respostas
- 8228 Exibições
- Última mensagem por Diego Silva

Ter Jul 23, 2013 18:11
Geometria Analítica
-
- [Vetor Unitario] questao de geometria analítica 1
por spektroos » Seg Set 24, 2012 01:41
- 2 Respostas
- 4015 Exibições
- Última mensagem por spektroos

Seg Set 24, 2012 16:52
Geometria Analítica
-
- [Vetor Unitario] Outra questao de geometria analítica 1
por spektroos » Seg Set 24, 2012 11:30
- 7 Respostas
- 5197 Exibições
- Última mensagem por spektroos

Seg Set 24, 2012 20:34
Geometria Analítica
-
- Geometria Analitica ( Vetor)
por raf » Qui Jun 11, 2015 03:46
- 1 Respostas
- 6925 Exibições
- Última mensagem por nakagumahissao

Sex Jun 12, 2015 15:37
Geometria Analítica
-
- vetor unitario
por andre barros » Sáb Mar 30, 2013 19:12
- 1 Respostas
- 1600 Exibições
- Última mensagem por e8group

Sáb Mar 30, 2013 20:50
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 33 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


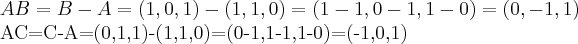

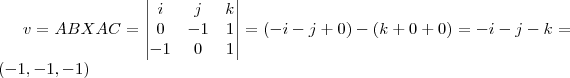
![{u}_{v}=(v/\left|v \right|)
\left|v \right|=\sqrt[]{(-1)^2+(-1)^2+(-1)^2}=\sqrt[]{3}
{u}_{v}=(-1/\sqrt[]{3},-1/\sqrt[]{3},-1/\sqrt[]{3}) {u}_{v}=(v/\left|v \right|)
\left|v \right|=\sqrt[]{(-1)^2+(-1)^2+(-1)^2}=\sqrt[]{3}
{u}_{v}=(-1/\sqrt[]{3},-1/\sqrt[]{3},-1/\sqrt[]{3})](/latexrender/pictures/8a0b1982884a18a22a9b88a180f1d008.png)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
