Primeiramente devo dizer que na primeira questão falta informação. Note que não é dito qual é o eixo de giro, ou seja, não é falado se devemos girar o segmento mantendo A fixo, ou B fixo, ou qualquer outro ponto. Vou supor que seja o ponto A.
- Quando giramos um segmneto de reta 90° horario ou anti-horario (geometrico no exercicio), estaremos produzindo um segundo segmento que é dito perpendicular ao primeiro (está a 90° do primeiro).
- Vamos começar calculando o coeficiente angular do primeiro segmento

:
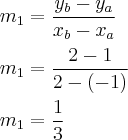
Calculamos este coeficiente, pois o coeficiente angular do segmento perpendicular deverá ser igual ao oposto inverso de
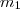
, ou seja,
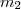
deverá ser igual a:

Obs.: Deixe em fração

Assim m2 deverá ser o coeficiente angular do segmento entre o ponto A e um C (ou D) que ainda não sabemos.
O coeficiente m2 pode ser calculado como feito anteriormente:

Agora o que podemos fazer é igualar os numeradores e igualar os denominadores para achar possiveis yc e xc.
- No entanto, note que temos um sinal (negativo) neste coeficiente, este sinal pode ser gerado de duas formas, numerador negativo e denominador positivo ou numerador positivo e denominador negativo.
- Estas duas possibilidades, exploradas logo abaixo, darão 2 yc's e 2 xc's diferentes, uma será para o giro horario e a outra para o giro anti-horario.
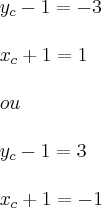
Resolvendo a primeira possibilidade temos:

Resolvendo a primeira possibilidade temos:

Espero ter ajudado, qualquer duvida deixe msg. Assim que puder tento resolver a outra questão (caso não tenham ainda).
Obs.: No desenho vermelho é o seg original, azul giro horario e verde anti-horario



 :
: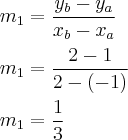
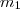 , ou seja,
, ou seja, 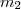 deverá ser igual a:
deverá ser igual a:

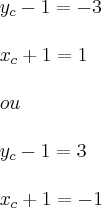



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.