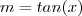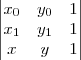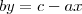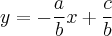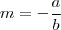Boa noite, espero que veja essa mensagem apesar da espera.
Se existem dois pontos
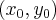
e

e esses formarem uma reta, é possível calcular o coeficiente angular
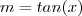
através de um
determinante, basta fazer:
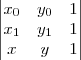
ao calcular o
determinante com tais valores, conseguirá a equação da reta geral, ou seja, na forma ax + by = c
Em seguida, isola-se o y:
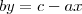
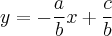
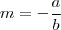


m é chamado de coeficiente angular e, equivale à tangente do ângulo entre a reta e o eixo das abscissas (x). Enquanto que n o coeficiente angular e corresponde à "altura" do ponto em que a reta cruza o eixo das ordenadas (y).
Logo, basta verificar a qual ângulo equivale a tangente encontrada, o que pode ser feito através de uma tabela ou da função inversa

a qual retornará um valor em radiano, logo, nesse caso, é necessário fazer a conversão para graus, caso seja necessário, caso contrário, verificar em uma tabela deve servir.
Espero ter ajudado.


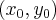 e
e