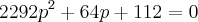raf,
Na sua resulução você multiplicou os vetores usando o PRODUTO ESCALAR. Porém, o que está sendo pedido é um PRODUTO VETORIAL e o mesmo deverá ser resolvido da seguinte maneira:
Dados os vetores u= (1, -3, -1), v= (3, 2, -1), w= (-1, 1, 3) e a= (k+1, 2k, -3k). Determine k de modo que [(u + v) x (w - v)] x a= 4
u + v = (1, -3, -1) + (3, 2, -1) = (1 + 3, -3 + 2, -1 -1) = (4, -1, -2)
w - v = (-1, 1, 3) - (3, 2, -1) = (-1 -3, 1 -2, 3 + 1) = (-4, -1, 4)
o Produto vetorial de (u + v) x (w - v) deverá ser:


Seja a= (p+1, 2p, -3p), onde p = k para que não existam confusões entre a variável k sendo procurada e o vetor k no determinante abaixo e ainda levando em consideração que o enunciado do problema esteja plenamente correto, teremos:
![[(u + v) \times (w - v)] \times a =
\begin{vmatrix}
i & j & k \\
-6 & -8 & -8 \\
p+1 & 2p & -3p
\end{vmatrix} = [(u + v) \times (w - v)] \times a =
\begin{vmatrix}
i & j & k \\
-6 & -8 & -8 \\
p+1 & 2p & -3p
\end{vmatrix} =](/latexrender/pictures/204fca09a1e77349fb4d45ce952198fb.png)

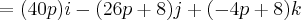
Novamente, considerando que o enunciado do problema esteja plenamente correto e levando em consideração que [(u + v) x (w - v)] x a= 4 onde o valor 4 é um valor escalar, suponho que a igualdade se dá através do cálculo do modúlo do vetor resultante do cálculo à esquerda da equação. Sendo assim:
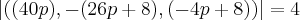
Calculando este módulo:
![\sqrt[]{1600p^2 + 676p^2 + 256p + 64 + 16p^2 - 64p + 64 } = 4 \sqrt[]{1600p^2 + 676p^2 + 256p + 64 + 16p^2 - 64p + 64 } = 4](/latexrender/pictures/7936e7069b624d639fc02d43c2b50a32.png)
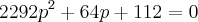
Resolvendo esta equação, teremos:
p = k =?0.0139661605584642234+0.22061435382981476i
p = k =?0.013961605584642234?0.22061435382981476i
Acredito que para um exercício, este resultado é muito estranho. Poderia verificar se o enunciado que passou está realmente correto por favor? Principalmente na parte:
[(u + v) x (w - v)] x a= 4
Em algum lugar nesta equação não seria um Ponto (.) representando o produto escalar em vez do sinal de Vezes (Produto vetorial)?
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali




![[(u + v) \times (w - v)] \times a =
\begin{vmatrix}
i & j & k \\
-6 & -8 & -8 \\
p+1 & 2p & -3p
\end{vmatrix} = [(u + v) \times (w - v)] \times a =
\begin{vmatrix}
i & j & k \\
-6 & -8 & -8 \\
p+1 & 2p & -3p
\end{vmatrix} =](/latexrender/pictures/204fca09a1e77349fb4d45ce952198fb.png)

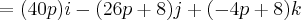
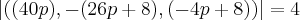
![\sqrt[]{1600p^2 + 676p^2 + 256p + 64 + 16p^2 - 64p + 64 } = 4 \sqrt[]{1600p^2 + 676p^2 + 256p + 64 + 16p^2 - 64p + 64 } = 4](/latexrender/pictures/7936e7069b624d639fc02d43c2b50a32.png)