Não sei se vai dá tempo de eu ver a resposta de vocês, mas estou desesperada. Será feita uma seleção
na minha faculdade, e a seleção consiste principalmente na didática do ensino de Geometria Analítica, e sendo assim,
foi nos proposto uma questão.
https://www.dropbox.com/s/bm5liyjh246qm ... .28.40.png (ENUNCIADO )
Reduzir cada uma das equacoes de forma a identificar a conica que ela representa e faca um
esboco do seu grafico:
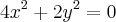
Pelo formato da equação, eu sei qe é uma elipse. Com a = 1/2 e b= 1/4.
com 2a = eixo maior, 2b = eixo menor, e c é a distância de um dos focos até o centro. Pois bem,
aprendi também que a distância de um dos focos até um dos pontos que representa o eixo menor, B1 ou B2, é a.
E a partir da trigonometria do triangulo retângulo, eu teria que c =
![\sqrt[]{{a}^{2} - {b}^{2}} \sqrt[]{{a}^{2} - {b}^{2}}](/latexrender/pictures/868709d46094c5b84bef0d1ebf515b7b.png) .
.Mas mesmo com as mesmas considerações em relação as representações, a resposta no livro tá c =
![\sqrt[]{{a}^{2} + {b}^{2}} \sqrt[]{{a}^{2} + {b}^{2}}](/latexrender/pictures/079fcb4bd5aca5306c9df751d3bcb470.png) . Então eu vi que c era a hipotenusa do triângulo no desenho entendi o porque, mas segundo as fontes que estudei, a hipotenusa, que é a distância de um foco até o B1 ou B2 é o a.
. Então eu vi que c era a hipotenusa do triângulo no desenho entendi o porque, mas segundo as fontes que estudei, a hipotenusa, que é a distância de um foco até o B1 ou B2 é o a.Poderiam olhar pra mim, por favor? Eu preciso muito.
Entrarei antes das 10hs da manhã pra verificar se houve respostas.
ESSA É A RESPOSTA DO EXERCICIO: https://www.dropbox.com/s/xk8o05jwk0wja ... .26.53.png
(Não sei se consegui explicar, mas eu quis dizer que meu c deu diferente. Tá dando
![\frac{1}{\sqrt[]{2}} \frac{1}{\sqrt[]{2}}](/latexrender/pictures/a708a9a9173a86197e94e74a716f2bea.png) )
)

 , somente na hiperbóle que é válida a relação
, somente na hiperbóle que é válida a relação  . Deve ter sido um erro na resposta msm.
. Deve ter sido um erro na resposta msm.
 Obrigada!
Obrigada!

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.