 por edilaine33 » Dom Dez 01, 2013 10:51
por edilaine33 » Dom Dez 01, 2013 10:51
gemetria analitica de vetores
- Anexos
-

-
edilaine33
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Nov 30, 2013 14:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em quimica
- Andamento: cursando
 por Bravim » Seg Dez 02, 2013 02:04
por Bravim » Seg Dez 02, 2013 02:04
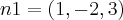
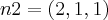

![\left|n1 \right|=\sqrt[]{1+4+9}=\sqrt[]{14} \left|n1 \right|=\sqrt[]{1+4+9}=\sqrt[]{14}](/latexrender/pictures/92fccc8a15d8b28bde31cae07afeff51.png)
![\left|n2 \right|=\sqrt[]{4+1+1}=\sqrt[]{6} \left|n2 \right|=\sqrt[]{4+1+1}=\sqrt[]{6}](/latexrender/pictures/8f336987008c2f4d17d6baa9a936b2ef.png)
![\left|v \right|=\sqrt[]{25+25+25}=\sqrt[]{75}=5*\sqrt[]{3} \left|v \right|=\sqrt[]{25+25+25}=\sqrt[]{75}=5*\sqrt[]{3}](/latexrender/pictures/6528162e35e1610f66ff5816d8146409.png)
![sin\theta=\frac{5*\sqrt[]{3}}{\sqrt[]{84}} sin\theta=\frac{5*\sqrt[]{3}}{\sqrt[]{84}}](/latexrender/pictures/34508c1a15159d1f997711960b317d12.png)
![sin\theta=\frac{2.5}{\sqrt[]{7}} sin\theta=\frac{2.5}{\sqrt[]{7}}](/latexrender/pictures/a54796712c748bba08d2d820befe710d.png)
Bem, percebi que seu professor errou a fórmula dada... no lugar onde ele botou cos ele deveria ter botado sin...
qualquer coisa consultar aqui:
http://pt.wikipedia.org/wiki/Produto_vetorial Bem de qualquer forma é bom se lembrar dos senos principais e tentar "chutar" um que saia mais ou menos perto
sin30°=0.5
sin45°=0.71
sin60°=0.87
O resultado da conta dá algo próximo de 0.94 então o resultado deve ser maior que 60 e menor que 90, logo só pode ser 71°
-

Bravim
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Qui Out 03, 2013 03:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7363 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
-
- [Vetores] Módulo e Versor de vetores
por LAZAROTTI » Sáb Set 22, 2012 22:42
- 1 Respostas
- 2988 Exibições
- Última mensagem por young_jedi

Sáb Set 22, 2012 22:50
Geometria Analítica
-
- [Vetores] Produto Entre Vetores
por _bruno94 » Qua Jul 10, 2013 00:34
- 1 Respostas
- 5206 Exibições
- Última mensagem por temujin

Qua Jul 10, 2013 14:27
Geometria Analítica
-
- [Vetores] Vetores iguais
por KleinIll » Dom Nov 04, 2012 12:17
- 2 Respostas
- 3401 Exibições
- Última mensagem por KleinIll

Dom Nov 04, 2012 13:50
Geometria Analítica
-
- [Vetores] Operações com vetores
por IlgssonBraga » Qui Jul 18, 2013 11:42
- 1 Respostas
- 2373 Exibições
- Última mensagem por Russman

Qui Jul 18, 2013 15:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



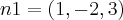
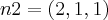

![\left|n1 \right|=\sqrt[]{1+4+9}=\sqrt[]{14} \left|n1 \right|=\sqrt[]{1+4+9}=\sqrt[]{14}](/latexrender/pictures/92fccc8a15d8b28bde31cae07afeff51.png)
![\left|n2 \right|=\sqrt[]{4+1+1}=\sqrt[]{6} \left|n2 \right|=\sqrt[]{4+1+1}=\sqrt[]{6}](/latexrender/pictures/8f336987008c2f4d17d6baa9a936b2ef.png)
![\left|v \right|=\sqrt[]{25+25+25}=\sqrt[]{75}=5*\sqrt[]{3} \left|v \right|=\sqrt[]{25+25+25}=\sqrt[]{75}=5*\sqrt[]{3}](/latexrender/pictures/6528162e35e1610f66ff5816d8146409.png)
![sin\theta=\frac{5*\sqrt[]{3}}{\sqrt[]{84}} sin\theta=\frac{5*\sqrt[]{3}}{\sqrt[]{84}}](/latexrender/pictures/34508c1a15159d1f997711960b317d12.png)
![sin\theta=\frac{2.5}{\sqrt[]{7}} sin\theta=\frac{2.5}{\sqrt[]{7}}](/latexrender/pictures/a54796712c748bba08d2d820befe710d.png)

