Perdi umas aulas, e não sei nem por onde começar...
Calcular o comprimento de arco da curva polar: O círculo inteiro r = a.
Ajudem, pf.



 uma curva no plano
uma curva no plano  . E suponha
. E suponha 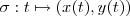 uma função vetorial de classe
uma função vetorial de classe  . Se
. Se  possui uma parametrização dada por
possui uma parametrização dada por  . Para pontos distintos
. Para pontos distintos 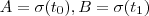 em
em  , temos que o comprimento do arco AB é dado por
, temos que o comprimento do arco AB é dado por 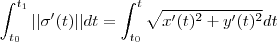 .
.  ser um circulo centrado na origem de raio
ser um circulo centrado na origem de raio  ,temos que
,temos que  é uma parametrização p/
é uma parametrização p/  .
.  e
e 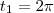 , obterá :
, obterá : 

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)