 por fyensinomedio » Sex Nov 08, 2013 13:04
por fyensinomedio » Sex Nov 08, 2013 13:04
O enunciado é : Um polígono regular de 16 lados tem o centro na origem e um de seus vértices está no ponto A=(0,1), Ache as equações das retas que passam pelo centro e por cada um de seus vértices.
Não consegui fazer muito.
Origem =(0,0). E pensei em fazer a determinante igual a zero entre ele e A.
Mas depois não consegui fazer mais nada.
-
fyensinomedio
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Nov 08, 2013 12:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Nov 08, 2013 20:38
por e8group » Sex Nov 08, 2013 20:38
Tenho uma dica que talvez possa ajudar .Comece notando que este polígono regular está inscrito em uma circunferência centrada na origem de raio 1 ,a princípio qualquer reta que passa pela origem intersectará o circulo em dois pontos que são simétricos em relação a origem (0,0) . Ora , se a reta passa pela origem , segue que seu coeficiente linear é zero e tendo conta seu coef. angular é dado por
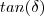
,escrevemos a forma geral da equação da reta

. Variando

em
![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png)
exceto nos pontos onde função tangente não estar definida que são
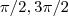
,obteremos infinitas retas que intersectam o circulo ,destas retas , 7 delas passará por pares de vértices do polígono regular .No total teremos 8 retas ,sendo incluída a reta

.
Espero que ajude . Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana] Polígono Regular
por edinaldoprof » Seg Fev 13, 2017 14:08
- 0 Respostas
- 2398 Exibições
- Última mensagem por edinaldoprof

Seg Fev 13, 2017 14:08
Geometria Plana
-
- Polígono regular
por Well » Seg Abr 16, 2012 19:47
- 0 Respostas
- 2015 Exibições
- Última mensagem por Well

Seg Abr 16, 2012 19:47
Geometria Plana
-
- [Geometria Espacial] Octaedro regular
 por rochadapesada » Qui Abr 11, 2013 18:15
por rochadapesada » Qui Abr 11, 2013 18:15
- 2 Respostas
- 6280 Exibições
- Última mensagem por rochadapesada

Dom Abr 14, 2013 17:33
Geometria Espacial
-
- UF-MG- Geometria. Determine a área do polígono
 por andersontricordiano » Qua Mar 16, 2011 16:43
por andersontricordiano » Qua Mar 16, 2011 16:43
- 8 Respostas
- 5268 Exibições
- Última mensagem por LuizAquino

Sáb Mar 26, 2011 10:21
Geometria Plana
-
- [GEOMETRIA] Calcular o lado de um polígono
por milenaponte » Qui Jun 11, 2015 12:15
- 2 Respostas
- 3128 Exibições
- Última mensagem por milenaponte

Qui Jun 11, 2015 21:39
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


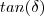 ,escrevemos a forma geral da equação da reta
,escrevemos a forma geral da equação da reta  . Variando
. Variando  em
em ![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) exceto nos pontos onde função tangente não estar definida que são
exceto nos pontos onde função tangente não estar definida que são 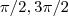 ,obteremos infinitas retas que intersectam o circulo ,destas retas , 7 delas passará por pares de vértices do polígono regular .No total teremos 8 retas ,sendo incluída a reta
,obteremos infinitas retas que intersectam o circulo ,destas retas , 7 delas passará por pares de vértices do polígono regular .No total teremos 8 retas ,sendo incluída a reta  .
.