Vamos pensar no gráfico de uma função do segundo grau, como a que o problema te dá. Ele é uma parábola. A parábola dessa equação, especificamente, é assim:

Os pontos

e

são os pontos onde a parábola intercepta o eixo

. O que isto significa? Significa que os pontos

e

são as raízes da sua equação, ou seja, os valores de

para que a equação dada resulta zero. E para achar o valor desses pontos, vamos usar a Fórmula de Bháskara.
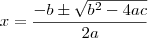
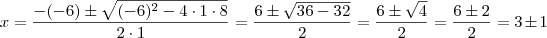
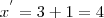
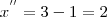
Pronto, achamos as coordenadas dos pontos

e

. O ponto

está nas coordenadas

e

em

.
Mas e o ponto

? O ponto

é o chamado vértice da parábola, é o seu ponto mais baixo (já que para cima ela prossegue infinitamente. Se a parábola fosse voltada para baixo, seu vértice seria seu ponto mais alto, já que para baixo ela seria infinita). Mas como calcular as coordenadas desse ponto? As coordenadas do vértice de uma função do segundo grau podem ser dadas por:


Lembrando que:

Então, mãos a obra e vamos achar as coordenadas do ponto V.
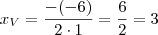

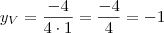
Sabemos as coordenadas do ponto

:

. Agora sim podemos calcular a área do triângulo
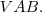

Como você deve saber, a fórmula da área do triângulo é:
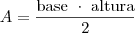
A base é a
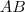
, ou seja, a distância entre os pontos

e

, que é

.
A altura

é a distância do ponto

ao eixo

(representada na imagem pela linha pontilhada), que é

.
Então:

Depois eu te ajudo com as outras, tô meio sem tempo agora (muita atividade de química) além do que ainda tô no 2º ano do ensino médio e ainda não estudei geometria analítica :s
Mas mesmo assim, espero ter ajudado! Se tiver ficado perdida em alguma parte é só falar (:



 e
e  são os pontos onde a parábola intercepta o eixo
são os pontos onde a parábola intercepta o eixo  . O que isto significa? Significa que os pontos
. O que isto significa? Significa que os pontos 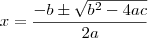
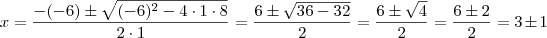
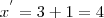
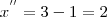
 e
e  .
.  ? O ponto
? O ponto 


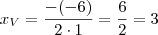

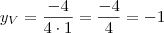
 . Agora sim podemos calcular a área do triângulo
. Agora sim podemos calcular a área do triângulo 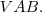

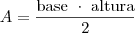
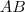 , ou seja, a distância entre os pontos
, ou seja, a distância entre os pontos  .
. é a distância do ponto
é a distância do ponto  .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  .
.
