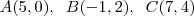por juxcarvalho » Dom Ago 18, 2013 10:09
por juxcarvalho » Dom Ago 18, 2013 10:09
1- Se M(2, 1), N(3, 3) e P(6, 2) são os pontos médios dos lados AB, BC e CA, respectivamente, de um triangulo ABC, determinar as coordenadas de A, B, e C.
2- O baricentro de um triângulo ABC é G(-4/3,4/3), o ponto médio do lado BC é N(-5/2,-1) e ponto médio do lado AB é M(0,1/2). Determine as coordenadas do vértice A, B e C.
Ooobg

-
juxcarvalho
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mai 30, 2013 11:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nakagumahissao » Qui Out 08, 2015 15:52
por nakagumahissao » Qui Out 08, 2015 15:52
![\frac{{x}_{1} + {x}_{2}}{2} = 2 \Rightarrow {x}_{1} + {x}_{2} = 4\;\;\;\;\;[1] \frac{{x}_{1} + {x}_{2}}{2} = 2 \Rightarrow {x}_{1} + {x}_{2} = 4\;\;\;\;\;[1]](/latexrender/pictures/abdc8d8babbb3235f2142534ae1f70ff.png)
![\frac{{x}_{2} + {x}_{3}}{2} = 3 \Rightarrow {x}_{2} + {x}_{3} = 6\;\;\;\;\;[2] \frac{{x}_{2} + {x}_{3}}{2} = 3 \Rightarrow {x}_{2} + {x}_{3} = 6\;\;\;\;\;[2]](/latexrender/pictures/69ea832fa7e21b51c1ca4f4860172018.png)
![\frac{{x}_{1} + {x}_{3}}{2} = 6 \Rightarrow {x}_{1} + {x}_{3} = 12\;\;\;\;\;[3] \frac{{x}_{1} + {x}_{3}}{2} = 6 \Rightarrow {x}_{1} + {x}_{3} = 12\;\;\;\;\;[3]](/latexrender/pictures/5271c09949a7c1aaa7d4bdfbe0184d19.png)
Destas equações obtemos:
De [1]:
![{x}_{1} + {x}_{2} = 4 \Leftrightarrow {x}_{1} = 4 - {x}_{2} \;\;\;\;[4] {x}_{1} + {x}_{2} = 4 \Leftrightarrow {x}_{1} = 4 - {x}_{2} \;\;\;\;[4]](/latexrender/pictures/d25bcc590cfcd061c7b72c1e1a8b73f0.png)
usando [4] em [3]:
![{x}_{1} + {x}_{3} = 12 \Leftrightarrow 4 - {x}_{2} + {x}_{3} = 12 \Leftrightarrow {x}_{3} = 8 + {x}_{2} \;\;\;\;[5] {x}_{1} + {x}_{3} = 12 \Leftrightarrow 4 - {x}_{2} + {x}_{3} = 12 \Leftrightarrow {x}_{3} = 8 + {x}_{2} \;\;\;\;[5]](/latexrender/pictures/55f514d18f1a6207e942a6de6bac8470.png)
Usando agora [5] em [2]:
![{x}_{2} + {x}_{3} = 6 \Rightarrow {x}_{2} + 8 + {x}_{2} = 6 \Rightarrow 2{x}_{2} = -2 \Rightarrow {x}_{2} = -1 \;\; [6] {x}_{2} + {x}_{3} = 6 \Rightarrow {x}_{2} + 8 + {x}_{2} = 6 \Rightarrow 2{x}_{2} = -2 \Rightarrow {x}_{2} = -1 \;\; [6]](/latexrender/pictures/00937ae505061c85db0dee833b9d55b6.png)
Usando o resultado [6] em [5]:
![{x}_{3} = 7 \;\;\;\;\;[7] {x}_{3} = 7 \;\;\;\;\;[7]](/latexrender/pictures/357495619e4427ba0c7902d851aa0eda.png)
Usando [7] em [4] obtem-se:
![{x}_{1} = 5 \;\;\;\;\;[8] {x}_{1} = 5 \;\;\;\;\;[8]](/latexrender/pictures/4f15f7e893ed9f097936ee2997e0aadc.png)
Resumindo:

Por um outro lado,
![\frac{{y}_{1} + {y}_{2}}{2} = 1 \Rightarrow {y}_{1} + {y}_{2} = 2 \Rightarrow {y}_{1} = 2 - {y}_{2} \;\;\;\;\;[9] \frac{{y}_{1} + {y}_{2}}{2} = 1 \Rightarrow {y}_{1} + {y}_{2} = 2 \Rightarrow {y}_{1} = 2 - {y}_{2} \;\;\;\;\;[9]](/latexrender/pictures/38f1c8b0ab2c70b56b7e3c423730099c.png)
![\frac{{y}_{2} + {y}_{3}}{2} = 3 \Rightarrow {y}_{2} + {y}_{3} = 6\;\;\;\;\;[10] \frac{{y}_{2} + {y}_{3}}{2} = 3 \Rightarrow {y}_{2} + {y}_{3} = 6\;\;\;\;\;[10]](/latexrender/pictures/793dbd201a4efd84f627a15f0ac38159.png)
![\frac{{y}_{1} + {y}_{3}}{2} = 2 \Rightarrow {y}_{1} + {y}_{3} = 4\;\;\;\;\;[11] \frac{{y}_{1} + {y}_{3}}{2} = 2 \Rightarrow {y}_{1} + {y}_{3} = 4\;\;\;\;\;[11]](/latexrender/pictures/382a3ae749016ad72dd3027795716271.png)
Usando [9] em [11]:
![{y}_{1} + {y}_{3} = 4 \Rightarrow 2 - {y}_{2} + {y}_{3} = 4 \Rightarrow {y}_{3} = 2 + {y}_{2}\;\;\;\;[12] {y}_{1} + {y}_{3} = 4 \Rightarrow 2 - {y}_{2} + {y}_{3} = 4 \Rightarrow {y}_{3} = 2 + {y}_{2}\;\;\;\;[12]](/latexrender/pictures/b079602a869a5b79cb933fe872bb05a2.png)
Usando este resultado [12] em [10], obtém-se:
![{y}_{2} + {y}_{3} = 6 \Rightarrow {y}_{2} + 2 + {y}_{2} = 6 \Rightarrow {y}_{2} = 2\;\;\;\;[13] {y}_{2} + {y}_{3} = 6 \Rightarrow {y}_{2} + 2 + {y}_{2} = 6 \Rightarrow {y}_{2} = 2\;\;\;\;[13]](/latexrender/pictures/3e9fb3e0aecd9bff378380a182a98597.png)
Usando [13] em [12], obtém-se:
![{y}_{3}= 4\;\;\;\;[14] {y}_{3}= 4\;\;\;\;[14]](/latexrender/pictures/4b25653843e300d213c039cf237e615b.png)
finalmente, utilizando [14] em [9], obtém-se:
![{y}_{1}= 0\;\;\;\;[15] {y}_{1}= 0\;\;\;\;[15]](/latexrender/pictures/0ef01c23a4f94a1e8e3e0f1cbcdaac9c.png)
temos até agora:


e os seguintes pontos:
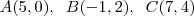
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ponto da reta r que é eqüidistante do ponto A e do ponto B
por gutorocher » Qua Jul 21, 2010 14:01
- 12 Respostas
- 15180 Exibições
- Última mensagem por gutorocher

Sex Jul 23, 2010 13:04
Geometria Analítica
-
- [Vetores] Ponto de reta próximo a outros pares de ponto
por cmcrz97 » Ter Jun 19, 2018 20:29
- 0 Respostas
- 2915 Exibições
- Última mensagem por cmcrz97

Ter Jun 19, 2018 20:29
Álgebra Linear
-
- [Ponto Crítico e Ponto de Inflexão e intervalos] Dúvidas em
por Andre Lopes » Qua Set 26, 2012 00:37
- 2 Respostas
- 3391 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 06:56
Cálculo: Limites, Derivadas e Integrais
-
- [ponto critico]duvida sobre achar o ponto critico
por nayra suelen » Dom Mai 27, 2012 19:38
- 2 Respostas
- 2449 Exibições
- Última mensagem por nayra suelen

Qua Mai 30, 2012 13:23
Cálculo: Limites, Derivadas e Integrais
-
- ponto simétrico
por sinuca147 » Seg Mai 25, 2009 09:40
- 3 Respostas
- 32322 Exibições
- Última mensagem por gustavoluiss

Seg Jan 03, 2011 02:03
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




![\frac{{x}_{1} + {x}_{2}}{2} = 2 \Rightarrow {x}_{1} + {x}_{2} = 4\;\;\;\;\;[1] \frac{{x}_{1} + {x}_{2}}{2} = 2 \Rightarrow {x}_{1} + {x}_{2} = 4\;\;\;\;\;[1]](/latexrender/pictures/abdc8d8babbb3235f2142534ae1f70ff.png)
![\frac{{x}_{2} + {x}_{3}}{2} = 3 \Rightarrow {x}_{2} + {x}_{3} = 6\;\;\;\;\;[2] \frac{{x}_{2} + {x}_{3}}{2} = 3 \Rightarrow {x}_{2} + {x}_{3} = 6\;\;\;\;\;[2]](/latexrender/pictures/69ea832fa7e21b51c1ca4f4860172018.png)
![\frac{{x}_{1} + {x}_{3}}{2} = 6 \Rightarrow {x}_{1} + {x}_{3} = 12\;\;\;\;\;[3] \frac{{x}_{1} + {x}_{3}}{2} = 6 \Rightarrow {x}_{1} + {x}_{3} = 12\;\;\;\;\;[3]](/latexrender/pictures/5271c09949a7c1aaa7d4bdfbe0184d19.png)
![{x}_{1} + {x}_{2} = 4 \Leftrightarrow {x}_{1} = 4 - {x}_{2} \;\;\;\;[4] {x}_{1} + {x}_{2} = 4 \Leftrightarrow {x}_{1} = 4 - {x}_{2} \;\;\;\;[4]](/latexrender/pictures/d25bcc590cfcd061c7b72c1e1a8b73f0.png)
![{x}_{1} + {x}_{3} = 12 \Leftrightarrow 4 - {x}_{2} + {x}_{3} = 12 \Leftrightarrow {x}_{3} = 8 + {x}_{2} \;\;\;\;[5] {x}_{1} + {x}_{3} = 12 \Leftrightarrow 4 - {x}_{2} + {x}_{3} = 12 \Leftrightarrow {x}_{3} = 8 + {x}_{2} \;\;\;\;[5]](/latexrender/pictures/55f514d18f1a6207e942a6de6bac8470.png)
![{x}_{2} + {x}_{3} = 6 \Rightarrow {x}_{2} + 8 + {x}_{2} = 6 \Rightarrow 2{x}_{2} = -2 \Rightarrow {x}_{2} = -1 \;\; [6] {x}_{2} + {x}_{3} = 6 \Rightarrow {x}_{2} + 8 + {x}_{2} = 6 \Rightarrow 2{x}_{2} = -2 \Rightarrow {x}_{2} = -1 \;\; [6]](/latexrender/pictures/00937ae505061c85db0dee833b9d55b6.png)
![{x}_{3} = 7 \;\;\;\;\;[7] {x}_{3} = 7 \;\;\;\;\;[7]](/latexrender/pictures/357495619e4427ba0c7902d851aa0eda.png)
![{x}_{1} = 5 \;\;\;\;\;[8] {x}_{1} = 5 \;\;\;\;\;[8]](/latexrender/pictures/4f15f7e893ed9f097936ee2997e0aadc.png)

![\frac{{y}_{1} + {y}_{2}}{2} = 1 \Rightarrow {y}_{1} + {y}_{2} = 2 \Rightarrow {y}_{1} = 2 - {y}_{2} \;\;\;\;\;[9] \frac{{y}_{1} + {y}_{2}}{2} = 1 \Rightarrow {y}_{1} + {y}_{2} = 2 \Rightarrow {y}_{1} = 2 - {y}_{2} \;\;\;\;\;[9]](/latexrender/pictures/38f1c8b0ab2c70b56b7e3c423730099c.png)
![\frac{{y}_{2} + {y}_{3}}{2} = 3 \Rightarrow {y}_{2} + {y}_{3} = 6\;\;\;\;\;[10] \frac{{y}_{2} + {y}_{3}}{2} = 3 \Rightarrow {y}_{2} + {y}_{3} = 6\;\;\;\;\;[10]](/latexrender/pictures/793dbd201a4efd84f627a15f0ac38159.png)
![\frac{{y}_{1} + {y}_{3}}{2} = 2 \Rightarrow {y}_{1} + {y}_{3} = 4\;\;\;\;\;[11] \frac{{y}_{1} + {y}_{3}}{2} = 2 \Rightarrow {y}_{1} + {y}_{3} = 4\;\;\;\;\;[11]](/latexrender/pictures/382a3ae749016ad72dd3027795716271.png)
![{y}_{1} + {y}_{3} = 4 \Rightarrow 2 - {y}_{2} + {y}_{3} = 4 \Rightarrow {y}_{3} = 2 + {y}_{2}\;\;\;\;[12] {y}_{1} + {y}_{3} = 4 \Rightarrow 2 - {y}_{2} + {y}_{3} = 4 \Rightarrow {y}_{3} = 2 + {y}_{2}\;\;\;\;[12]](/latexrender/pictures/b079602a869a5b79cb933fe872bb05a2.png)
![{y}_{2} + {y}_{3} = 6 \Rightarrow {y}_{2} + 2 + {y}_{2} = 6 \Rightarrow {y}_{2} = 2\;\;\;\;[13] {y}_{2} + {y}_{3} = 6 \Rightarrow {y}_{2} + 2 + {y}_{2} = 6 \Rightarrow {y}_{2} = 2\;\;\;\;[13]](/latexrender/pictures/3e9fb3e0aecd9bff378380a182a98597.png)
![{y}_{3}= 4\;\;\;\;[14] {y}_{3}= 4\;\;\;\;[14]](/latexrender/pictures/4b25653843e300d213c039cf237e615b.png)
![{y}_{1}= 0\;\;\;\;[15] {y}_{1}= 0\;\;\;\;[15]](/latexrender/pictures/0ef01c23a4f94a1e8e3e0f1cbcdaac9c.png)