 por Sohrab » Ter Abr 16, 2013 20:24
por Sohrab » Ter Abr 16, 2013 20:24
Olá caros..
estava estudando as interseções de planos y = k no parabolóide hiperbólico de equação

e neste material de estudo, dizia que essa interseção seria a parábola

de retas focais paralelas ao eixo -OZ, vértice no ponto
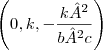
e concavidade voltada para cima, para

, uma vez que a²c é < 0...
minha dúvida é entender como ele achou o vértice dessa parábola. podem me dar uma força?
obrigado e abraços!!
-
Sohrab
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Mar 18, 2010 17:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Téc. em Mec. Usinagem e Info Programação
- Andamento: cursando
 por Sohrab » Qua Abr 17, 2013 00:40
por Sohrab » Qua Abr 17, 2013 00:40
obs: ignorem esses  que sairam nas fôrmulas. não sei porque aconteceu isso. não apareciam no editor de latex...
-
Sohrab
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Mar 18, 2010 17:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Téc. em Mec. Usinagem e Info Programação
- Andamento: cursando
 por young_jedi » Qua Abr 17, 2013 11:39
por young_jedi » Qua Abr 17, 2013 11:39
sendo a equação da parabola igual a
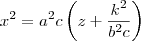
então
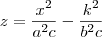
esta é uma equação da forma

onde o vertice é

da nossa equação nos temos que B=0 portanto
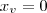
pra achar
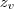
é so substituir o valor de x

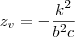
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Quádricas] Prova de reta contida em paraboloide hiperbólico
por GFerraz » Seg Abr 24, 2017 20:37
- 0 Respostas
- 4244 Exibições
- Última mensagem por GFerraz

Seg Abr 24, 2017 20:37
Geometria Analítica
-
- Paraboloide
por Man Utd » Qua Jul 31, 2013 16:30
- 2 Respostas
- 4688 Exibições
- Última mensagem por Man Utd

Qui Ago 01, 2013 19:12
Geometria Analítica
-
- paraboloide
 por gvt123 » Qui Jun 18, 2020 18:12
por gvt123 » Qui Jun 18, 2020 18:12
- 0 Respostas
- 1942 Exibições
- Última mensagem por gvt123

Qui Jun 18, 2020 18:12
Geometria Analítica
-
- Calculo dos angulos internos dum triangulo hiperbólico
por Jhenrique » Ter Jul 24, 2012 18:42
- 0 Respostas
- 1817 Exibições
- Última mensagem por Jhenrique

Ter Jul 24, 2012 18:42
Geometria Espacial
-
- [Parábolas]
por Ana_Rodrigues » Seg Nov 21, 2011 14:16
- 2 Respostas
- 2245 Exibições
- Última mensagem por Ana_Rodrigues

Seg Nov 21, 2011 19:29
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


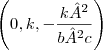 e concavidade voltada para cima, para
e concavidade voltada para cima, para  , uma vez que a²c é < 0...
, uma vez que a²c é < 0...

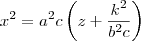
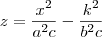


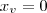
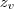 é so substituir o valor de x
é so substituir o valor de x
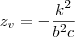


 .
.



