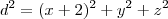e do ponto P = (-2,0,0). Que conjunto é esse?
e do ponto P = (-2,0,0). Que conjunto é esse?Sei o que é lugar geométrico. E sei também encontrar e qual é o ''formato'' da equação de um plano. Mas não sei como aplicar essas informações no problema... O exercício indica que é uma cônica uma quádrica. Grato a quem puder ajudar !