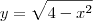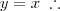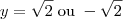por jeffersonricardo » Seg Set 06, 2010 08:46
por jeffersonricardo » Seg Set 06, 2010 08:46
plote num mesmo sistema de eixos a reta e a circunferência e verifique a posição da reta em relação à circunferência, e se forem concorrentes, calcule os pontos de intersecção .
y=x
x*x+y*y=4
como vou saber se e concorrente?
não conseguir fazer alguem pode me ajudar
-
jeffersonricardo
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Ago 16, 2010 15:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletronica e de telecunicaçao
- Andamento: cursando
 por jeffersonricardo » Seg Set 06, 2010 10:32
por jeffersonricardo » Seg Set 06, 2010 10:32
Douglasm
seria sim
desculpe foi a pressa
vc pode me ajudar
estou com duvida neste exercicio
-
jeffersonricardo
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Ago 16, 2010 15:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletronica e de telecunicaçao
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [circunferência] Questão de reta secante a circunferência
por danielleecb » Qui Jun 07, 2012 23:26
- 1 Respostas
- 1868 Exibições
- Última mensagem por MarceloFantini

Sex Jun 08, 2012 12:24
Geometria Analítica
-
- Reta que intercepta uma circunferência
por Stella » Ter Nov 18, 2014 18:45
- 0 Respostas
- 1182 Exibições
- Última mensagem por Stella

Ter Nov 18, 2014 18:45
Geometria Analítica
-
- [Reta e Circunferência] UESB 2011.2
por Leocondeuba » Ter Nov 05, 2013 22:05
- 0 Respostas
- 1054 Exibições
- Última mensagem por Leocondeuba

Ter Nov 05, 2013 22:05
Geometria Analítica
-
- [Geometria Analítica] Reta Tangente a Circunferência
por RasecAlmeida » Qui Out 16, 2014 13:57
- 1 Respostas
- 1801 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:19
Geometria Analítica
-
- geometria analítica estudo da reta distancia do ponta à reta
por jeffersonricardo » Dom Ago 22, 2010 08:29
- 1 Respostas
- 2408 Exibições
- Última mensagem por Pedro123

Seg Ago 23, 2010 22:24
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.