 por Jonatan » Sex Jul 30, 2010 21:25
por Jonatan » Sex Jul 30, 2010 21:25
Forneça a equação da circunferência simétrica de

em relação ao eixo das ordenadas.
Gabarito:
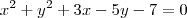
Como se resolve essa questão?
Eu comecei a resolvê-la descobrindo as coordenadas do centro bem como o raio da circunferência dada, e achei a seguinte equação reduzida de circunferência:

Em que as coordenadas do centro são:

Em que o raio é: R = 3
Entretanto, a partir de agora, não sei mais como fazer o exercício. Alguém pode resolver para mim e me explicar como se faz esse tipo de questão? Desde já, agradeço.
-
Jonatan
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Jun 16, 2010 13:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Jul 31, 2010 14:40
por MarceloFantini » Sáb Jul 31, 2010 14:40
Qual é o ponto simétrico em relação ao eixo das ordenadas do ponto

? Se você resolver esse, analogamente resolverá o da circunferência.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 em relação ao eixo das ordenadas.
em relação ao eixo das ordenadas.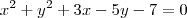




 ? Se você resolver esse, analogamente resolverá o da circunferência.
? Se você resolver esse, analogamente resolverá o da circunferência.


 .
.



