 por Jonatan » Qua Jul 07, 2010 11:32
por Jonatan » Qua Jul 07, 2010 11:32
Determine as equações das retas que formam 45º com o eixo dos x e estão à distância
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
do ponto P (3,4).
Pessoal, tentei fazer o seguinte:
Para uma reta:
y = ax + b
y = 1x + b (pois o a é o coeficiente angular, tg

= a e no caso do execício,
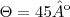
; tg 45º = 1)
Como as retas estão com inclinação de 45º em relação ao eixo dos x, trata-se de uma função identidade, em que o coeficiente linear é nulo e o coeficiente angular é 1).
E a outra reta, como faz?
Alguém pode resolver o exercício para mim, passo-a-passo? Estou com dúvidas nessa parte da matéria, estudo sozinho e fica meio complicado. Se alguém puder ajudar, agradeço.
-
Jonatan
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Jun 16, 2010 13:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Douglasm » Qua Jul 07, 2010 18:33
por Douglasm » Qua Jul 07, 2010 18:33
Olá Jonatan. Primeiramente sabemos que o coeficiente angular de ambas as retas é 1. Deste modo, eu fiz um desenho para ilustrar a situação:

- retas.jpg (8.37 KiB) Exibido 3321 vezes
(Conto com a sua boa vontade em verificar que os triângulos azuis possuem lados

,

e

)
Por conta disso, podemos encontrar os pontos de intersecção entre a reta que passa pelo ponto P e pelas duas retas. Evidentemente os pontos são (2,5) e (4,3). Finalmente é só determinarmos as retas:
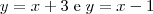
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Tom » Qui Jul 08, 2010 00:53
por Tom » Qui Jul 08, 2010 00:53
A resolução do Douglas está correta. Segue abaixo outro método para obter o mesmo resultado usando a técnica de
translação:
Defina um sistema de coordenadas retangulares auxiliar
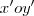
com origem no ponto
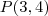
. Para esse sistema, a equação da circunferência em questão é :
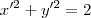
. Ao passo que no sistema de coordenadas convencional a equação seria

Note que a equivalência translacional é, portanto:

e
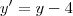
Ainda para o sistema
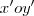
, como as retas que queremos achar possuem coeficiente angular igual a

, basta verificar a intercessão com a circunferência supracitada fazendo

; assim obtemos :

e, respeitando a posição dos eixos definidos obtemos os referidos pontos de intercessão
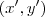
a saber:
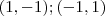
Decorre assim que a equação das retas é:

e

Aplicando, agora, a equivalência translacional entre eixos:
Se

, isto é,

Se

, isto é,
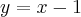
Assim, no sistema de coordenadas convencional

as retas em questão são:
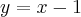
e

Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por MarceloFantini » Qui Jul 08, 2010 17:09
por MarceloFantini » Qui Jul 08, 2010 17:09
E existe a terceira resolução (que é bom que seja a última a ser apresentada) que é usando a fórmula de distância de ponto a reta;

Logo,

ou

Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Tom » Sex Jul 09, 2010 00:21
por Tom » Sex Jul 09, 2010 00:21
Fantini escreveu:(que é bom que seja a última a ser apresentada)
Uai ?

Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por MarceloFantini » Sex Jul 09, 2010 11:20
por MarceloFantini » Sex Jul 09, 2010 11:20
Para que ele não se prenda a fórmulas e aprenda a pensar e ver outros jeitos de resolver.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Distância de ponto à reta
por Jonatan » Qua Jul 07, 2010 11:24
- 1 Respostas
- 2719 Exibições
- Última mensagem por Tom

Qua Jul 07, 2010 13:11
Geometria Analítica
-
- Reta distancia ponto
por felipe grion » Seg Fev 20, 2012 10:41
- 1 Respostas
- 1723 Exibições
- Última mensagem por LuizAquino

Seg Fev 20, 2012 11:43
Geometria Analítica
-
- Distância ponto-reta
por ViniciusAlmeida » Seg Ago 24, 2015 21:03
- 1 Respostas
- 3530 Exibições
- Última mensagem por nakagumahissao

Sex Set 11, 2015 11:32
Geometria Analítica
-
- [Distância de Ponto a Reta]
por anselmojr97 » Qui Abr 07, 2016 00:18
- 0 Respostas
- 1313 Exibições
- Última mensagem por anselmojr97

Qui Abr 07, 2016 00:18
Geometria Analítica
-
- distancia de ponto a reta ajuda aew
por Fabricio dalla » Seg Mai 02, 2011 17:34
- 1 Respostas
- 1338 Exibições
- Última mensagem por LuizAquino

Sex Mai 20, 2011 21:48
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) do ponto P (3,4).
do ponto P (3,4). = a e no caso do execício,
= a e no caso do execício, 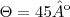 ; tg 45º = 1)
; tg 45º = 1)

 ,
,  e
e 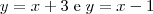

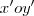 com origem no ponto
com origem no ponto 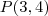 . Para esse sistema, a equação da circunferência em questão é :
. Para esse sistema, a equação da circunferência em questão é : 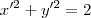 . Ao passo que no sistema de coordenadas convencional a equação seria
. Ao passo que no sistema de coordenadas convencional a equação seria 
 e
e 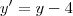
 ; assim obtemos :
; assim obtemos :  e, respeitando a posição dos eixos definidos obtemos os referidos pontos de intercessão
e, respeitando a posição dos eixos definidos obtemos os referidos pontos de intercessão 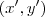 a saber:
a saber: 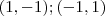
 e
e 
 , isto é,
, isto é, 
 , isto é,
, isto é, 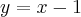
 as retas em questão são:
as retas em questão são: 

 ou
ou 





 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.