 por Lucio Martins » Qua Mai 12, 2010 19:34
por Lucio Martins » Qua Mai 12, 2010 19:34
Em uma piramide quadrangular regular a aresta lateral mede 5 cm a e altura mede 4 cm . o volume em cubico ( cm3) é:
-
Lucio Martins
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qua Mai 05, 2010 20:58
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por Molina » Qua Mai 12, 2010 19:50
por Molina » Qua Mai 12, 2010 19:50
Lucio Martins escreveu:Em uma piramide quadrangular regular a aresta lateral mede 5 cm a e altura mede 4 cm . o volume em cubico ( cm3) é:
Boa noite.
Use a fórmula do Volume:
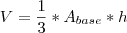
A altura você tem. A área da base é fácil descobrir pois é informado o lado do quadrado.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Douglasm » Qui Mai 13, 2010 12:12
por Douglasm » Qui Mai 13, 2010 12:12
Olá Lúcio. É como o Molina disse, use a fórmula do volume. Só cuidado quando for determinar a área da base, pois é fornecida a aresta lateral e não o lado da base. Usando o teorema de Pitágoras você pode determinar metade da diagonal da base e, ai sim, descobrir o lado do quadrado. Desenhe com cuidado que não tem erro.
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Mai 13, 2010 21:05
por MarceloFantini » Qui Mai 13, 2010 21:05
Se é uma pirâmide quadrangular regular, supostamente todas as arestas são iguais. O enunciado deveria ter dito "pirâmide de base quadrangular regular".
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Douglasm » Qui Mai 13, 2010 22:03
por Douglasm » Qui Mai 13, 2010 22:03
Pirâmide regular é uma pirâmide cuja base é um polígono regular e a projeção ortogonal do vértice sobre o plano da base é o centro da base. Numa pirâmide regular as arestas laterais são congruentes e as faces laterais são triângulos
isósceles congruentes .
Essa é a definição formal que encontrei no livro (Fundamentos da Matemática Elementar 10). Eu não creio que o fato da pirâmide ser regular implique que todas as arestas sejam iguais. Mas vamos testar:
Supondo que todas as arestas são iguais e fazendo o que eu disse anteriormente, vamos verificar que é uma afirmação falsa: (d = diagonal do quadrado)
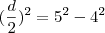

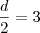
Deste modo a diagonal
d é igual a 6, e o lado do quadrado é
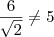
.
Num caso geral de pirâmide quadrangular regular, pode-se verificar que as arestas (representadas aqui por
x) só serão todas iguais quando
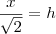
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Mai 13, 2010 22:11
por MarceloFantini » Qui Mai 13, 2010 22:11
Eu já havia feito a verificação aqui pra confirmar, mas não sabia a definição precisa de pirâmide regular. Obrigado pelo esclarecimento!
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Douglasm » Qui Mai 13, 2010 22:15
por Douglasm » Qui Mai 13, 2010 22:15
Já me confundi bastante em outros tempos, por isso é tão importante a definição formal para que não erremos mais!
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria
por ehrefundini » Ter Abr 22, 2008 16:53
- 3 Respostas
- 7326 Exibições
- Última mensagem por admin

Qui Mai 01, 2008 15:57
Pedidos de Materiais
-
- geometria 2
por ehrefundini » Qua Mai 07, 2008 10:35
- 1 Respostas
- 6041 Exibições
- Última mensagem por admin

Qua Mai 07, 2008 10:59
Pedidos de Materiais
-
- Geometria
por rybb » Ter Ago 25, 2009 07:48
- 1 Respostas
- 2872 Exibições
- Última mensagem por Elcioschin

Seg Out 05, 2009 22:41
Trigonometria
-
- Geometria - help me?
por rybb » Ter Ago 25, 2009 07:55
- 3 Respostas
- 7317 Exibições
- Última mensagem por Molina

Qua Ago 26, 2009 23:18
Geometria
-
- geometria
por cristina » Qui Nov 19, 2009 07:05
- 0 Respostas
- 2468 Exibições
- Última mensagem por cristina

Qui Nov 19, 2009 07:05
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



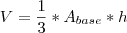





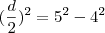

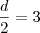
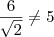 .
.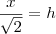




 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
