2- O baricentro de um triângulo ABC é G(-4/3,4/3), o ponto médio do lado BC é N(-5/2,-1) e ponto médio do lado AB é M(0,1/2). Determine as coordenadas do vértice A, B e C.
Ooobg




![\frac{{x}_{1} + {x}_{2}}{2} = 2 \Rightarrow {x}_{1} + {x}_{2} = 4\;\;\;\;\;[1] \frac{{x}_{1} + {x}_{2}}{2} = 2 \Rightarrow {x}_{1} + {x}_{2} = 4\;\;\;\;\;[1]](/latexrender/pictures/abdc8d8babbb3235f2142534ae1f70ff.png)
![\frac{{x}_{2} + {x}_{3}}{2} = 3 \Rightarrow {x}_{2} + {x}_{3} = 6\;\;\;\;\;[2] \frac{{x}_{2} + {x}_{3}}{2} = 3 \Rightarrow {x}_{2} + {x}_{3} = 6\;\;\;\;\;[2]](/latexrender/pictures/69ea832fa7e21b51c1ca4f4860172018.png)
![\frac{{x}_{1} + {x}_{3}}{2} = 6 \Rightarrow {x}_{1} + {x}_{3} = 12\;\;\;\;\;[3] \frac{{x}_{1} + {x}_{3}}{2} = 6 \Rightarrow {x}_{1} + {x}_{3} = 12\;\;\;\;\;[3]](/latexrender/pictures/5271c09949a7c1aaa7d4bdfbe0184d19.png)
![{x}_{1} + {x}_{2} = 4 \Leftrightarrow {x}_{1} = 4 - {x}_{2} \;\;\;\;[4] {x}_{1} + {x}_{2} = 4 \Leftrightarrow {x}_{1} = 4 - {x}_{2} \;\;\;\;[4]](/latexrender/pictures/d25bcc590cfcd061c7b72c1e1a8b73f0.png)
![{x}_{1} + {x}_{3} = 12 \Leftrightarrow 4 - {x}_{2} + {x}_{3} = 12 \Leftrightarrow {x}_{3} = 8 + {x}_{2} \;\;\;\;[5] {x}_{1} + {x}_{3} = 12 \Leftrightarrow 4 - {x}_{2} + {x}_{3} = 12 \Leftrightarrow {x}_{3} = 8 + {x}_{2} \;\;\;\;[5]](/latexrender/pictures/55f514d18f1a6207e942a6de6bac8470.png)
![{x}_{2} + {x}_{3} = 6 \Rightarrow {x}_{2} + 8 + {x}_{2} = 6 \Rightarrow 2{x}_{2} = -2 \Rightarrow {x}_{2} = -1 \;\; [6] {x}_{2} + {x}_{3} = 6 \Rightarrow {x}_{2} + 8 + {x}_{2} = 6 \Rightarrow 2{x}_{2} = -2 \Rightarrow {x}_{2} = -1 \;\; [6]](/latexrender/pictures/00937ae505061c85db0dee833b9d55b6.png)
![{x}_{3} = 7 \;\;\;\;\;[7] {x}_{3} = 7 \;\;\;\;\;[7]](/latexrender/pictures/357495619e4427ba0c7902d851aa0eda.png)
![{x}_{1} = 5 \;\;\;\;\;[8] {x}_{1} = 5 \;\;\;\;\;[8]](/latexrender/pictures/4f15f7e893ed9f097936ee2997e0aadc.png)

![\frac{{y}_{1} + {y}_{2}}{2} = 1 \Rightarrow {y}_{1} + {y}_{2} = 2 \Rightarrow {y}_{1} = 2 - {y}_{2} \;\;\;\;\;[9] \frac{{y}_{1} + {y}_{2}}{2} = 1 \Rightarrow {y}_{1} + {y}_{2} = 2 \Rightarrow {y}_{1} = 2 - {y}_{2} \;\;\;\;\;[9]](/latexrender/pictures/38f1c8b0ab2c70b56b7e3c423730099c.png)
![\frac{{y}_{2} + {y}_{3}}{2} = 3 \Rightarrow {y}_{2} + {y}_{3} = 6\;\;\;\;\;[10] \frac{{y}_{2} + {y}_{3}}{2} = 3 \Rightarrow {y}_{2} + {y}_{3} = 6\;\;\;\;\;[10]](/latexrender/pictures/793dbd201a4efd84f627a15f0ac38159.png)
![\frac{{y}_{1} + {y}_{3}}{2} = 2 \Rightarrow {y}_{1} + {y}_{3} = 4\;\;\;\;\;[11] \frac{{y}_{1} + {y}_{3}}{2} = 2 \Rightarrow {y}_{1} + {y}_{3} = 4\;\;\;\;\;[11]](/latexrender/pictures/382a3ae749016ad72dd3027795716271.png)
![{y}_{1} + {y}_{3} = 4 \Rightarrow 2 - {y}_{2} + {y}_{3} = 4 \Rightarrow {y}_{3} = 2 + {y}_{2}\;\;\;\;[12] {y}_{1} + {y}_{3} = 4 \Rightarrow 2 - {y}_{2} + {y}_{3} = 4 \Rightarrow {y}_{3} = 2 + {y}_{2}\;\;\;\;[12]](/latexrender/pictures/b079602a869a5b79cb933fe872bb05a2.png)
![{y}_{2} + {y}_{3} = 6 \Rightarrow {y}_{2} + 2 + {y}_{2} = 6 \Rightarrow {y}_{2} = 2\;\;\;\;[13] {y}_{2} + {y}_{3} = 6 \Rightarrow {y}_{2} + 2 + {y}_{2} = 6 \Rightarrow {y}_{2} = 2\;\;\;\;[13]](/latexrender/pictures/3e9fb3e0aecd9bff378380a182a98597.png)
![{y}_{3}= 4\;\;\;\;[14] {y}_{3}= 4\;\;\;\;[14]](/latexrender/pictures/4b25653843e300d213c039cf237e615b.png)
![{y}_{1}= 0\;\;\;\;[15] {y}_{1}= 0\;\;\;\;[15]](/latexrender/pictures/0ef01c23a4f94a1e8e3e0f1cbcdaac9c.png)


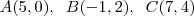

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)