Determine a equaç?o da reta que passa pelo ponto (1,-3) e é perpendicular à reta 2x - 3y +6 = 0
Alguém pode me ajudar?



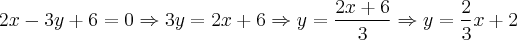
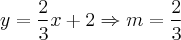

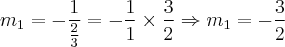
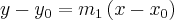
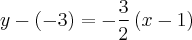

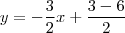



nakagumahissao escreveu:Reescrevendo a equação da reta data, ficará:
Olhando para a equação que temos agora, vemos que a inclinação desta reta, que chamaremos de m é:
Para que uma reta seja perpendicular à outra,
Então, a inclinação da reta perpendicular à reta dada será:
Como nos foi fornecido um ponto das duas retas por onde nossa reta perpendicular deverá passar, então teremos como equação da reta perpendicular que passa por este ponto (1, -3) como sendo:
Finalmente,
que é a equação da reta perpendicular à reta data 2x - 3y + 6 = 0 e que passa pelo ponto (1, -3).


Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)