 por GES » Seg Mai 04, 2015 02:26
por GES » Seg Mai 04, 2015 02:26
Boa noite. Peço por gentileza que me deem uma luz nesta questão.
QUESTÃO: os vetores u= (2,1,-1) e v=(1,-1,m+1) formam um ângulo de 45º entre si. Calcule o valor de m.
usei a formula de angulos entre vetores: cosseno de teta igual a u escalar v sobre o produto dos modulos de u e v;
cheguei na equação quadrática: 8m² + 40m + 68 = 0 ; Isso me deu um delta igual a -576. A matemática diz que não existe raiz quadrada real para número negativo. Desejo se possível, que alguém me informe se cometi algum erro ou se meus números estão certos. obrigado.
-
GES
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 05, 2015 22:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciência e tecnologia
- Andamento: cursando
 por DanielFerreira » Sex Mai 08, 2015 00:06
por DanielFerreira » Sex Mai 08, 2015 00:06
Olá
GES, boa noite!
Fiz da seguinte forma:

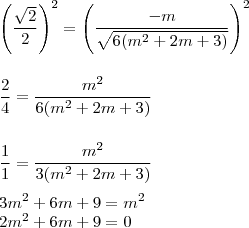
De fato
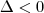
; digitaste correctamente os vetores?
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por GES » Sex Mai 08, 2015 00:41
por GES » Sex Mai 08, 2015 00:41
amigo, muito obrigado pela ajuda. Os vetores estão corretos. Essa questão foi feita para dar uma raiz negativa, mesmo. mais uma vez obrigado.
-
GES
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 05, 2015 22:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciência e tecnologia
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Incógnita de logaritmo
por usuariomatematica » Ter Mai 31, 2011 09:18
- 0 Respostas
- 1677 Exibições
- Última mensagem por usuariomatematica

Ter Mai 31, 2011 09:18
Logaritmos
-
- Denominador com incógnita
por TAE » Ter Mai 29, 2012 16:33
- 3 Respostas
- 5726 Exibições
- Última mensagem por Molina

Ter Mai 29, 2012 20:55
Sistemas de Equações
-
- Potência com incógnita
por Lana Brasil » Ter Abr 09, 2013 16:45
- 3 Respostas
- 3147 Exibições
- Última mensagem por Lana Brasil

Ter Abr 09, 2013 20:22
Álgebra Elementar
-
- [Isolar incógnita]
por malukaopba2018 » Ter Mar 27, 2018 06:54
- 2 Respostas
- 4670 Exibições
- Última mensagem por malukaopba2018

Qua Mar 28, 2018 07:08
Equações
-
- .Soma de Matrizes com Incógnita (FGV).
por obamathiaxx » Dom Jun 12, 2011 17:13
- 1 Respostas
- 3244 Exibições
- Última mensagem por LuizAquino

Dom Jun 12, 2011 17:21
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



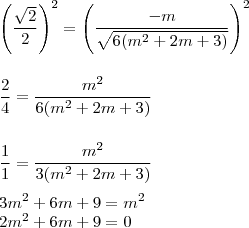
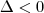 ; digitaste correctamente os vetores?
; digitaste correctamente os vetores?
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.