pelos dados do problema,temos q.
os ptos 0,A,B,C sao vertices de um pararalepido,mas o pto O,nao pertence a fase definida pelos ptos A,B,C...
pelo proprio enunciado podemops ter:D(0,0,1)eixo-z,E(0,1,0)eixo-y do pararalelpipedo,e esses ptos com os ptos dados sao suficientes p/resoluçao...
no primeiro octante temos:
ABCD definem uma face,OABE definem a fase no plano xy,logo...
os vetores OB,OC definem um plano diagonal,e AE,AC definem a outro plano diagonal...
logo,
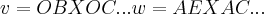
sao os vetores normais a esses planos diagonais...entao...

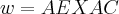
=
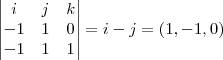
,entao...

![cos(v,w)=1.1+(-1).(-1)+1.0/(\sqrt[]{3}.\sqrt[]{2})= cos(v,w)=1.1+(-1).(-1)+1.0/(\sqrt[]{3}.\sqrt[]{2})=](/latexrender/pictures/68a2bc55b7507d5a3f69352809cd0c13.png)
![\Rightarrow (v,w)=arcos(2/\sqrt[]{6}) \Rightarrow (v,w)=arcos(2/\sqrt[]{6})](/latexrender/pictures/52795b8c43a3c54360ce1e469d5a9834.png)




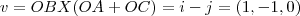
![seja o plano determ.por AC, cujo vetor normal eh:
[tex]w=OBX(OC-OA)=i-j+2k=(1,-1,2) seja o plano determ.por AC, cujo vetor normal eh:
[tex]w=OBX(OC-OA)=i-j+2k=(1,-1,2)](/latexrender/pictures/a1d2c926a7ceed7103f4e906b61c2b62.png) ...entao:
...entao:![v.w=\left|v \right|\left|w \right|cos(v,w)\Rightarrow cos(v,w)=v.w/(\left|v \right|.\left|w \right|)=(1,-1,0)(1,-1,2)/(2\sqrt[]{2})=1+1+0/2\sqrt[]{2}=1/\sqrt[]{2}=\sqrt[]{2}/2\Rightarrow (v,w)=arcos(\sqrt[]{2}/2)=\pi/4\Rightarrow (v,w)=45° v.w=\left|v \right|\left|w \right|cos(v,w)\Rightarrow cos(v,w)=v.w/(\left|v \right|.\left|w \right|)=(1,-1,0)(1,-1,2)/(2\sqrt[]{2})=1+1+0/2\sqrt[]{2}=1/\sqrt[]{2}=\sqrt[]{2}/2\Rightarrow (v,w)=arcos(\sqrt[]{2}/2)=\pi/4\Rightarrow (v,w)=45°](/latexrender/pictures/cdb2dc20405deb088f6caa6a079e8315.png)


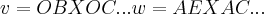 sao os vetores normais a esses planos diagonais...entao...
sao os vetores normais a esses planos diagonais...entao...
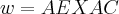 =
=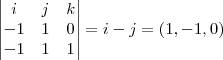 ,entao...
,entao...
![cos(v,w)=1.1+(-1).(-1)+1.0/(\sqrt[]{3}.\sqrt[]{2})= cos(v,w)=1.1+(-1).(-1)+1.0/(\sqrt[]{3}.\sqrt[]{2})=](/latexrender/pictures/68a2bc55b7507d5a3f69352809cd0c13.png)
![\Rightarrow (v,w)=arcos(2/\sqrt[]{6}) \Rightarrow (v,w)=arcos(2/\sqrt[]{6})](/latexrender/pictures/52795b8c43a3c54360ce1e469d5a9834.png)


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)