Suponha que as curvas se encontrem em um ponto genérico
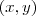
. Se isto é verdade, então este ponto pertence as duas curvas simultaneamente! Assim, monta-se um sistema de equações
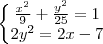
pois o ponto
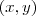
deve satisfazer ambas equações.
Esse sistema não-linear pode ser resolvido com substituição. Multiplique a 1° equação por 2 e substitua o

da equação de baixo.
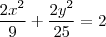

---> Só pra eliminar as frações
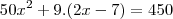
---> efetuamos a substituição

Obtivemos uma equação de 2° grau para a ordenada x do ponto. Esta equação possui duas raízes reais! Isto é, ainda existe a possibilidade de encontro entre as curvas. Porém, se você calcular estas raízes verá que elas encontram-se em um intervalo(aproximado)
![[-3,4;3,03] [-3,4;3,03]](/latexrender/pictures/36f212a56df5dd81f0151c2f9e4d69ea.png)
o que não gera raízes reais para y!
Da segunda equação, como para todo y é necessário que
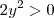
, temos
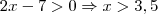
.
Assim, as raízes da equação obtida para x não estão dentro do intervalo necessário para a existência de y real!
Portanto tal ponto de encontro não existe.
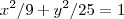 e da parábola
e da parábola  .
.

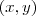 . Se isto é verdade, então este ponto pertence as duas curvas simultaneamente! Assim, monta-se um sistema de equações
. Se isto é verdade, então este ponto pertence as duas curvas simultaneamente! Assim, monta-se um sistema de equações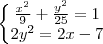
 da equação de baixo.
da equação de baixo.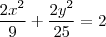
 ---> Só pra eliminar as frações
---> Só pra eliminar as frações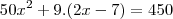 ---> efetuamos a substituição
---> efetuamos a substituição
![[-3,4;3,03] [-3,4;3,03]](/latexrender/pictures/36f212a56df5dd81f0151c2f9e4d69ea.png) o que não gera raízes reais para y!
o que não gera raízes reais para y!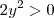 , temos
, temos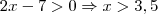 .
.